题目内容
(本小题12分)已知函数 的图象在
的图象在 轴上的截距为1,在相邻两最值点
轴上的截距为1,在相邻两最值点 ,
, 上
上 分别取得最大值和最小值.
分别取得最大值和最小值.
⑴求 的解析式;
的解析式;
⑵若函数 满足方程
满足方程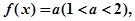 求在
求在 内的所有实数根之和.
内的所有实数根之和.
 的图象在
的图象在 轴上的截距为1,在相邻两最值点
轴上的截距为1,在相邻两最值点 ,
, 上
上 分别取得最大值和最小值.
分别取得最大值和最小值.⑴求
 的解析式;
的解析式;⑵若函数
 满足方程
满足方程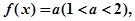 求在
求在 内的所有实数根之和.
内的所有实数根之和.(1) (2)21.
(2)21.
 (2)21.
(2)21.(1)先根据 ,
, ,再根据最值得A=2,因为图像过点(0,1),求出
,再根据最值得A=2,因为图像过点(0,1),求出 ,到此解析式确定.
,到此解析式确定.
(2)解本题的关键是把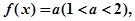 在
在 内的所有实数根的问题转化为y=f(x)与y=a在[0,9]范围内有几个交点的问题.由于
内的所有实数根的问题转化为y=f(x)与y=a在[0,9]范围内有几个交点的问题.由于 的周期
的周期 ,∴函数
,∴函数 在
在 上恰好是三个周期.函数
上恰好是三个周期.函数 与
与 在在
在在 内有6个交点.
内有6个交点.
解:(1)依题意,得:
 ,
, …………2分
…………2分
最大值为2,最小值为-2,
 …………4分
…………4分
图象经过 ,
, ,即
,即
又
 ,
, …………6分
…………6分
(2)∵ 的周期
的周期 ,∴函数
,∴函数 在
在 上恰好是三个周期.函数
上恰好是三个周期.函数 与
与 在在
在在 内有6个交点.…………8分由于函数
内有6个交点.…………8分由于函数 的图象具有对称性,数形结合可知:方程
的图象具有对称性,数形结合可知:方程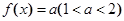 有6个实数根.且前两个根关于直线
有6个实数根.且前两个根关于直线 对称,所以前两根之和1.………10分
对称,所以前两根之和1.………10分
再由周期性可知:中间两根之和为1+6=7,后两根之和为1+12=13………11分
所以方程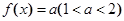 在
在 内的所有实数根之和为1+7+13=21.……12分
内的所有实数根之和为1+7+13=21.……12分
 ,
, ,再根据最值得A=2,因为图像过点(0,1),求出
,再根据最值得A=2,因为图像过点(0,1),求出 ,到此解析式确定.
,到此解析式确定.(2)解本题的关键是把
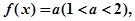 在
在 内的所有实数根的问题转化为y=f(x)与y=a在[0,9]范围内有几个交点的问题.由于
内的所有实数根的问题转化为y=f(x)与y=a在[0,9]范围内有几个交点的问题.由于 的周期
的周期 ,∴函数
,∴函数 在
在 上恰好是三个周期.函数
上恰好是三个周期.函数 与
与 在在
在在 内有6个交点.
内有6个交点.解:(1)依题意,得:
 ,
, …………2分
…………2分最大值为2,最小值为-2,

 …………4分
…………4分图象经过
 ,
, ,即
,即
又

 ,
, …………6分
…………6分(2)∵
 的周期
的周期 ,∴函数
,∴函数 在
在 上恰好是三个周期.函数
上恰好是三个周期.函数 与
与 在在
在在 内有6个交点.…………8分由于函数
内有6个交点.…………8分由于函数 的图象具有对称性,数形结合可知:方程
的图象具有对称性,数形结合可知:方程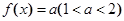 有6个实数根.且前两个根关于直线
有6个实数根.且前两个根关于直线 对称,所以前两根之和1.………10分
对称,所以前两根之和1.………10分再由周期性可知:中间两根之和为1+6=7,后两根之和为1+12=13………11分
所以方程
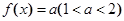 在
在 内的所有实数根之和为1+7+13=21.……12分
内的所有实数根之和为1+7+13=21.……12分
练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 ,且其图象关于直线
,且其图象关于直线 对称,则( )
对称,则( )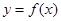 的最小正周期为
的最小正周期为 ,且在
,且在 上为增函数
上为增函数 ,且在
,且在 上为增函数
上为增函数 .
. 的值;
的值; 的值.
的值. ,且
,且 是第二象限角,求
是第二象限角,求 的值。
的值。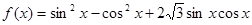 。求函数
。求函数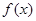 的单调递增区间和最小值;
的单调递增区间和最小值; ,
, .
. 的最大值;
的最大值;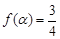 ,求
,求 的值.
的值. 为周期的偶函数是( ).
为周期的偶函数是( ).



 )
)  )
)
 ,则
,则 ( )
( )

 或
或
 或
或