题目内容
【题目】p：方程x2+2mx+1＝0有两个不相等的正根，q：不等式m2﹣m﹣6＜0成立；求使p∨q为真，p∧q为假时，实数m的取值范围．
【答案】（﹣∞，﹣2]∪[﹣1，1]∪[3，+∞）
【解析】
由p：方程x2+2mx+1＝0有两个不相等的正根，解出m的取值范围，由q：不等式m2﹣m﹣6＜0成立，解出m的取值范围，再由p∨q为真，p∧q为假，可知p与q一真一假，由此可解得m的取值范围．
p：方程x2+2mx+1＝0有两个不相等的正根，则△＝4m2﹣4＞0，解得m＞1或m＜﹣1；
q：不等式m2﹣m﹣6＜0成立，则﹣2＜m＜3，
若p∨q为真，p∧q为假时，则命题p与命题q一真一假，
当p真q假时，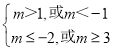
，解得m≤﹣2或m≥3，
当q真p假时，
，解得﹣1≤m≤1，
综上，实数m的取值范围（﹣∞，﹣2]∪[﹣1，1]∪[3，+∞）．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
