Question

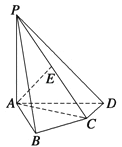
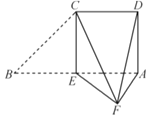
【题目】如图，在△MBC中，MA是BC边上的高，MA＝3，AC＝4，将△MBC沿MA进行翻折，使得∠BAC＝90°如图，再过点B作BD∥AC，连接AD，CD，MD且，∠CAD＝30°．

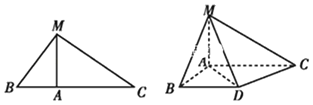
（1）求证：平面MCD⊥平面MAD；

（2）求点B到平面MAD的距离．

Answer 1

【答案】（1）见解析； （2）.

【解析】

(1)证明CD⊥平面MAD即可.

(2)利用等体积法 VB﹣MAD＝VM﹣BAD,再求出,利用三棱锥的体积公式求解即可.

（1）因为MA是BC边上的高,所以MA⊥AB,MA⊥AC,

又因为AB平面ABDC,AC平面ABDC,AB∩AC＝A,

所以MA⊥平面ABDC,则MA⊥CD,MA⊥AD,

在Rt△ADM中,MD,

在Rt△ACM中,MC5,

在△ACD中,由余弦定理可得CD2,

则在△CDM中,CD2+DM2＝CM2,即有△CDM是直角三角形,所以CD⊥DM,

又因为CD⊥AM,AM平面MAD,DM平面MAD,AM∩DM＝M,

所以CD⊥平面MAD,又因为CD平面MCD,所以平面MCD⊥平面MAD；

（2）在△BAD中,∠BAD＝60°,AD＝2,则AB,BD＝3,所以,

又因为MA⊥AD,所以3,

因为MA⊥平面ABDC,即MA⊥平面BAD,则VB﹣MAD＝VM﹣BAD,

即3,解得d,

即点B到平面MAD的距离为．