题目内容
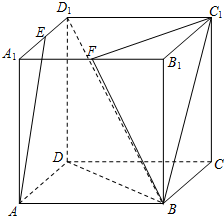 如图,在正方体ABCD-A1B1C1D1中,E、F分别是A1D1和A1B1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是A1D1和A1B1的中点.(1)求异面直线AE和BF所成角的余弦值;
(2)求平面BDD1与平面BFC1所成二面角的正弦值.
分析:(1)以A为坐标原点,AB,AD,AA1分别为X,Y,Z轴正方向,建立空间坐标系,分别求出异面直线AE和BF的方向向量,代入向量夹角公式,即可求出异面直线AE和BF所成角的余弦值;
(2)分别求出平面BDD1与平面BFC1的法向量,代入向量夹角公式,我们可以求出平面BDD1与平面BFC1所成二面角的余弦值,进而根据同角三角函数关系,可以求出平面BDD1与平面BFC1所成二面角的正弦值.
(2)分别求出平面BDD1与平面BFC1的法向量,代入向量夹角公式,我们可以求出平面BDD1与平面BFC1所成二面角的余弦值,进而根据同角三角函数关系,可以求出平面BDD1与平面BFC1所成二面角的正弦值.
解答:解:以A为坐标原点,AB,AD,AA1分别为X,Y,Z轴正方向,建立空间坐标系,
设正方体ABCD-A1B1C1D1的棱长为2,
则A(0,0,0),B(2,0,0),E(0,1,2),F(1,0,2),C1(2,2,2)
(1)则
=(0,1,2),
=(-1,0,2)
设异面直线AE和BF所成角为θ
则cosθ=|
|=
即异面直线AE和BF所成角的余弦值为
(2)∵
=(2,0,0)为平面BDD1的一个法向量,
设向量
=(x,y,z)为平面BFC1的一个法向量
则
,即
令z=1,则向量
=(2,-1,1)为平面BFC1的一个法向量
∵cos<
,
>=
=
∴sin<
,
>=
∴平面BDD1与平面BFC1所成二面角的正弦值为
设正方体ABCD-A1B1C1D1的棱长为2,
则A(0,0,0),B(2,0,0),E(0,1,2),F(1,0,2),C1(2,2,2)
(1)则
| AE |
| BF |
设异面直线AE和BF所成角为θ
则cosθ=|
| ||||
|
|
| 4 |
| 5 |
即异面直线AE和BF所成角的余弦值为
| 4 |
| 5 |
(2)∵
| AB |
设向量
| n |
则
|
|
令z=1,则向量
| n |
∵cos<
| n |
| AB |
| ||||
|
|
| ||
| 3 |
∴sin<
| n |
| AB |
| ||
| 3 |
∴平面BDD1与平面BFC1所成二面角的正弦值为
| ||
| 3 |
点评:本题考查的知识点是二面角的平面角及求法,异面直线及其所成的角,其中建立空间坐标系,将二面角问题及异面直线夹角问题转化为向量夹角问题是解答本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记
如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点, 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )