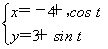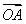Question

设命题p：非零向量a，b，|a|＝|b|是(a＋b)⊥(a－b)的充要条件；命题q：平面上M为一动点，A，B，C三点共线的充要条件是存在角α，使＝sin2α＋cos2α，下列命题①p∧q；②p∨q；③?p∧q；④?p∨q.

其中假命题的序号是________．(将所有假命题的序号都填上)

 

Answer 1

①③④

【解析】(a＋b)⊥(a－b)?(a＋b)·(a－b)＝a2－b2＝|a|2－|b|2＝0?|a|＝|b|，故p是真命题．

若A，B，C三点共线，则存在x，y∈R，

使＝x ＋y (x＋y＝1)；

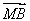若＝sin2α＋cos2α，则A，B，C三点共线．

故q是假命题．

故p∧q，?p∧q，?p∨q为假命题．