题目内容
已知曲线C1：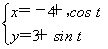
(t为参数)，C2：
(θ为参数)．
(1)化C1、C2的方程为普通方程，并说明它们分别表示什么曲线；
(2)若C1上的点P对应的参数为t＝
，Q为C2上的动点，求PQ中点M到直线C3：
(t为参数)距离的最小值．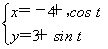
解
（1）C1为圆心是(－4,3)，半径是1的圆．C2为中心是坐标原点，焦点在x轴上，长半轴长是8，短半轴长是3的椭圆．（2）
【解析】(1)C1：(x＋4)2＋(y－3)2＝1，C2：
＝1.
C1为圆心是(－4,3)，半径是1的圆．
C2为中心是坐标原点，焦点在x轴上，长半轴长是8，短半轴长是3的椭圆．
(2)当t＝
时，P(－4,4)，Q(8cos θ，3sin θ)，
故M
.
C3为直线x－2y－7＝0，M到C3的距离
d＝
|4cos θ－3sin θ－13|.
从而当cos θ＝
，sin θ＝－
时，d取得最小值.
练习册系列答案
相关题目
