题目内容
椭圆C: =1(a>b>0)的左、右焦点分别是F1、F2,离心率为
=1(a>b>0)的左、右焦点分别是F1、F2,离心率为 ,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
(1)求椭圆C的方程;
(2)点P是椭圆C上除长轴端点外的任一点,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点.设直线PF1,PF2的斜率分别为k1,k2.若k≠0,试证明 +
+ 为定值,并求出这个定值.
为定值,并求出这个定值.
(1)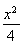 +y2=1.(2)
+y2=1.(2)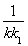 +
+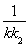 为定值,这个定值为-8
为定值,这个定值为-8
【解析】(1)由于c2=a2-b2,将x=-c代入椭圆方程 =1,得y=±
=1,得y=± .
.
由题意知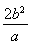 =1,即a=2b2.
=1,即a=2b2.
又e=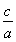 =
=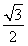 ,所以a=2,b=1.所以椭圆C的方程为
,所以a=2,b=1.所以椭圆C的方程为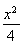 +y2=1.
+y2=1.
(2)设P(x0,y0)(y0≠0),又F1(-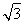 ,0),F2(
,0),F2(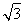 ,0),
,0),
知 ,
,
直线l的方程为y-y0=k(x-x0).联立得
整理得(1+4k2)x2+8(ky0-k2x0)x+4( -2kx0y0+k2
-2kx0y0+k2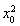 -1)=0.
-1)=0.
由题意Δ=0,即(4-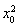 )k2+2x0y0k+1-
)k2+2x0y0k+1- =0.
=0.
又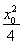 +
+ =1,
=1,
所以16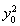 k2+8x0y0k+
k2+8x0y0k+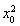 =0,故k=-
=0,故k=- .
.
所以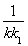 +
+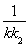 =
= =
=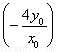 ·
·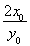 =-8,
=-8,
因此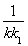 +
+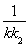 为定值,这个定值为-8
为定值,这个定值为-8

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目






















