题目内容
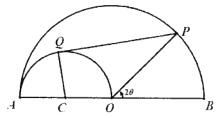
【题目】在直角坐标系xOy中，曲线E的参数方程为
（
为参数），以O为极点，x轴非负半轴为极轴建立极坐标系，直线
，
的极坐标方程分别为
，
，交曲线E于点A，B，交曲线E于点C，D.
（1）求曲线E的普通方程及极坐标方程；
（2）求
的值.
【答案】（1）
；
（2）16
【解析】
（1）由同角的平方关系可得曲线E的普通方程；由x＝ρcosθ，y＝ρsinθ，x2+y2＝ρ2，代入化简可得曲线E的极坐标方程；
（2）分别讨论直线l1的斜率不存在，求得A，B，C，D的坐标，计算可得所求和；若斜率存在且不为0，设出两直线的方程，联立圆的方程，运用韦达定理，以及两直线垂直的条件，结合两点的距离公式可得所求和．
解：（1）由E的参数方程
（
为参数），知曲线E是以
为圆心，半径为2的圆，
∴曲线E的普通方程为
令
，
得
，
即曲线E极坐标方程为
（2）依题意得
，根据勾股定理，
，
将
，
代入中，
得
，
设点A，B，C，D所对应的极径分别为
，
，
，
，
则
，
，
，
∴
练习册系列答案
相关题目
