题目内容
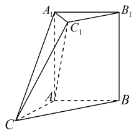
【题目】如图所示的几何体![]() 中,四边形
中,四边形![]() 是正方形,四边形
是正方形,四边形![]() 是梯形,
是梯形,![]()
![]()
![]() ,且
,且![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,二面角
,二面角![]() 为
为![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
(Ⅰ)取![]() 的中点
的中点![]() ,可得,由
,可得,由![]() 平面
平面![]() 平面
平面![]() 得
得![]() 平面
平面![]() ,所以
,所以![]() ,从而得
,从而得![]() 平面
平面![]() ,可得
,可得![]() 、
、![]() 为平行四边形,所以
为平行四边形,所以![]() ,所以
,所以![]() 平面
平面![]() ,再得到平面
,再得到平面![]() 平面
平面![]() ;
;
(Ⅱ)以![]() 为原点,建立空间直角坐标系,设
为原点,建立空间直角坐标系,设![]() ,求出平面
,求出平面![]() 和平面
和平面![]() 的法向量,再利用向量的夹角公式,得到关于
的法向量,再利用向量的夹角公式,得到关于![]() 的方程,求出
的方程,求出![]() 的值,从而得到
的值,从而得到![]() 的值.
的值.
(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]()
∵![]() 是正方形,∴
是正方形,∴![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]()
又∵![]() 平面
平面![]() ,∴
,∴![]()
又![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]()
∵![]() ,且
,且![]() ,
,
∴![]() ,
,![]()
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,![]()
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]()
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]()

(Ⅱ)由(Ⅰ)得,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
设![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
易知平面![]() 的一个法向量为
的一个法向量为![]()
设![]() 为平面
为平面![]() 的法向量,由
的法向量,由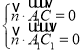 得
得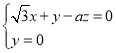 ,
,
令![]() ,得
,得![]()
∴![]() ,解得
,解得![]() ,
,
∴![]()

【题目】BMI指数(身体质量指数,英文为BodyMassIndex,简称BMI)是衡量人体胖瘦程度的一个标准,BMI=体重(kg)/身高(m)的平方.根据中国肥胖问题工作组标准,当BMI≥28时为肥胖.某地区随机调查了1200名35岁以上成人的身体健康状况,其中有200名高血压患者,被调查者的频率分布直方图如下:
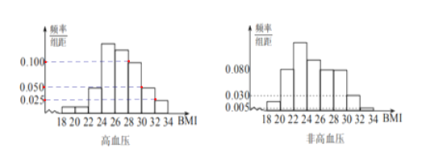
(1)求被调查者中肥胖人群的BMI平均值![]() ;
;
(2)填写下面列联表,并判断是否有99.9%的把握认为35岁以上成人患高血压与肥胖有关.
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
肥胖 | 不肥胖 | 合计 | |
高血压 | |||
非高血压 | |||
合计 |
附: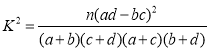 ,
,![]()
【题目】某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(Ⅰ)请估计该市公众对“车辆限行”的赞成率和被调查者的年龄平均值;
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记被选4人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)若在这50名被调查者中随机发出20份的调查问卷,记![]() 为所发到的20人中赞成“车辆限行”的人数,求使概率
为所发到的20人中赞成“车辆限行”的人数,求使概率![]() 取得最大值的整数
取得最大值的整数![]() .
.