Question

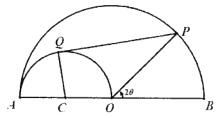
【题目】某广告商租用了一块如图所示的半圆形封闭区域用于产品展示,该封闭区域由以为圆心的半圆及直径围成．在此区域内原有一个以为直径、为圆心的半圆形展示区,该广告商欲在此基础上,将其改建成一个凸四边形的展示区,其中、分别在半圆与半圆的圆弧上,且与半圆相切于点．已知长为40米,设为．（上述图形均视作在同一平面内）

（1）记四边形的周长为,求的表达式;

（2）要使改建成的展示区的面积最大,求的值．

Answer 1

【答案】（1）,．（2）

【解析】

（1）由余弦定理的,然后根据直线与圆相切的性质求出,从而求出;

（2）求得的表达式,通过求导研究函数的单调性求得最大值.

解：（1）连．由条件得．

在三角形中,,,,由余弦定理,得

,

因为与半圆相切于,所以,

所以,所以．

所以四边形的周长为

,．

（2）设四边形的面积为,则

,．

所以,．

令,得

列表：

	+	0	-
	增	最大值	减

答：要使改建成的展示区的面积最大,的值为．