题目内容
【题目】记不等式组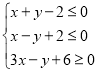 ,表示的平面区域为
,表示的平面区域为![]() .下面给出的四个命题:
.下面给出的四个命题:![]() ;
;![]() ;
;![]() ;
;![]() 其中真命题的是:
其中真命题的是:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
由约束条件作出可行域,利用目标函数的几何意义求解z=x+y,z1=2x﹣y,z2![]() ,z3=x2+y2,的范围,判断命题的真假即可.
,z3=x2+y2,的范围,判断命题的真假即可.
实数x,y满足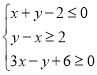 ,由约束条件作出可行域为D,如图阴影部分,
,由约束条件作出可行域为D,如图阴影部分,
A(﹣2,0),B(0,2),C(﹣1,3),z=x+y经过可行域的点A及直线BC时分别取得最值,可得:z∈[﹣2,2],所以![]() 错误;
错误;
z1=2x﹣y经过可行域的B、C时分别取得最值,可得:z1∈[﹣5,﹣2],所以![]() 正确;
正确;
z2![]() ,它的几何意义是可行域内的点与(1,﹣1)连线的斜率,
,它的几何意义是可行域内的点与(1,﹣1)连线的斜率,
可得:DA的斜率是最大值为:![]() ;
;
BD的斜率取得最小值为:![]() ;z2∈[
;z2∈[![]() ,
,![]() ];所以
];所以![]() 错误;
错误;
z3=x2+y2,它的几何意义是可行域内的点与(0,0)连线的距离的平方,
最小值为原点到直线y=x+2的距离的平方:(![]() )2
)2![]() ,最大值为OC的平方:(﹣1﹣0)2+(3﹣0)2=10,z3∈[
,最大值为OC的平方:(﹣1﹣0)2+(3﹣0)2=10,z3∈[![]() ,10].所以
,10].所以![]() 正确;
正确;
故选:C.

练习册系列答案
相关题目
【题目】随着移动互联网的发展,越来越多的人习惯用手机应用程序(简称app)获取新闻资讯.为了解用户对某款新闻类app的满意度,随机调查了300名用户,调研结果如表:(单位:人)
青年人 | 中年人 | 老年人 | |
满意 | 60 | 70 | x |
一般 | 55 | 25 | y |
不满意 | 25 | 5 | 10 |
(1)从所有参与调研的人中随机选取1人,估计此人“不满意”的概率;
(2)从参与调研的青年人和中年人中各随机选取1人,估计恰有1人“满意”的概率;
(3)现需从参与调研的老年人中选择6人作进一步访谈,若在“满意”、“一般”、“不满意”的老年人中各取2人,这种抽样是否合理?说明理由.