题目内容
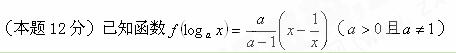
(1)求
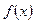 解析式并判断
解析式并判断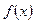 的奇偶性;
的奇偶性;(2)对于(1)中的函数
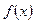 ,若
,若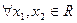 当
当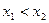 时都有
时都有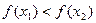 成立,求满足条件
成立,求满足条件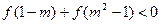 的实数m的取值范围。
的实数m的取值范围。解:⑴令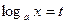 ,则
,则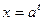
∴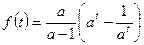
∴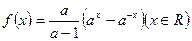 -----------------------------------------------4分
-----------------------------------------------4分
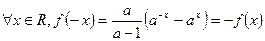
∴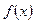 为奇函数-------------------6分
为奇函数-------------------6分
⑵依题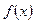 在R上单调递增---
在R上单调递增--- ---------------------------8分
---------------------------8分
由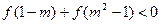 得
得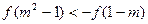 又
又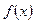 为奇函数
为奇函数
∴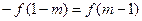 即
即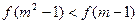 -----------------
----------------- ------------
------------ -10分
-10分
由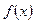 在R上单调递增得
在R上单调递增得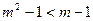 即
即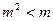 解得0
解得0 <m<1
<m<1
故实数m的取值范围为(0,1)------------------------ ------12分
------12分
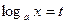 ,则
,则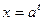
∴
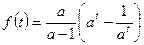
∴
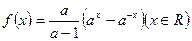 -----------------------------------------------4分
-----------------------------------------------4分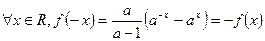
∴
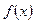 为奇函数-------------------6分
为奇函数-------------------6分⑵依题
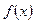 在R上单调递增---
在R上单调递增--- ---------------------------8分
---------------------------8分由
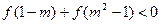 得
得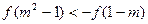 又
又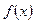 为奇函数
为奇函数∴
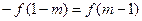 即
即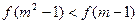 -----------------
----------------- ------------
------------ -10分
-10分由
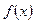 在R上单调递增得
在R上单调递增得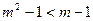 即
即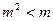 解得0
解得0 <m<1
<m<1故实数m的取值范围为(0,1)------------------------
 ------12分
------12分略

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
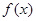 是
是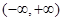 上的偶函数,若对于
上的偶函数,若对于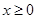 ,都有
,都有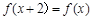 ,且当
,且当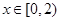 时,
时,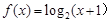 ,则
,则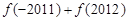 的值为
的值为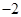
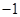
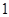
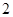
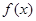 定义域为R,则
定义域为R,则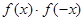 一定为 (
一定为 ( 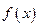 是定义在R上的奇函数,若
是定义在R上的奇函数,若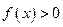 。则以下不等式不一定成立的是 ( )
。则以下不等式不一定成立的是 ( )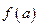 >
>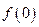
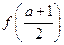 >
>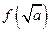
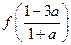 >
>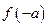
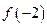
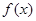 在
在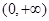 上是增函数,且
上是增函数,且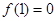 ,则不等式
,则不等式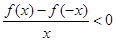
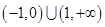
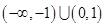
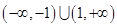
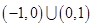
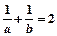 ,则A=____
,则A=____ ____。
____。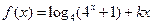
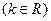 是偶函数,则
是偶函数,则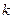 的值为
的值为 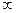 )上是减函数,如果
)上是减函数,如果 且| x1 | < | x2 | , 则有( )
且| x1 | < | x2 | , 则有( )