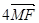题目内容
已知对任意平面向量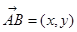 ,把
,把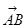 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转 角得到向量
角得到向量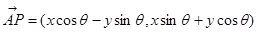 ,叫做把点
,叫做把点 绕点
绕点 逆时针方向旋转角得到点
逆时针方向旋转角得到点 。
。
(1)已知平面内点 ,点
,点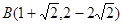 。把点
。把点 绕点
绕点 沿逆时针旋转
沿逆时针旋转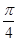 后得到点
后得到点 ,求点
,求点 的坐标;
的坐标;
(2)设平面内直线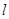 上的每一点绕坐标原点沿逆时针方向旋转
上的每一点绕坐标原点沿逆时针方向旋转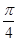 后得到的点组成的直线方程是
后得到的点组成的直线方程是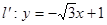 ,求原来的直线
,求原来的直线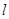 方程。
方程。
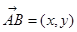 ,把
,把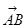 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转 角得到向量
角得到向量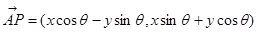 ,叫做把点
,叫做把点 绕点
绕点 逆时针方向旋转角得到点
逆时针方向旋转角得到点 。
。(1)已知平面内点
 ,点
,点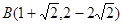 。把点
。把点 绕点
绕点 沿逆时针旋转
沿逆时针旋转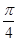 后得到点
后得到点 ,求点
,求点 的坐标;
的坐标;(2)设平面内直线
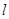 上的每一点绕坐标原点沿逆时针方向旋转
上的每一点绕坐标原点沿逆时针方向旋转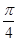 后得到的点组成的直线方程是
后得到的点组成的直线方程是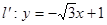 ,求原来的直线
,求原来的直线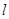 方程。
方程。(1)(0,-1)
(2)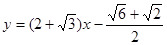 .
.
(2)
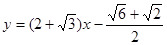 .
.试题分析:利用题中的新定义,可先计算
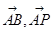 ,结合已知A(1,2),利用向量的减法,可求P点坐标.根据题意,由于
,结合已知A(1,2),利用向量的减法,可求P点坐标.根据题意,由于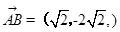
 绕点
绕点 沿逆时针旋转
沿逆时针旋转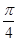 后得到点
后得到点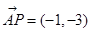 ∵A(1,2),∴P(0,-1 )故答案为:(0,-1)
∵A(1,2),∴P(0,-1 )故答案为:(0,-1)(2)根据新定义可知,如果平面内直线
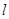 上的每一点绕坐标原点沿逆时针方向旋转
上的每一点绕坐标原点沿逆时针方向旋转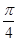 后得到的点组成的直线方程是
后得到的点组成的直线方程是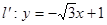 ,那么可知原来的直线
,那么可知原来的直线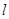 方程
方程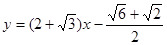
点评:本题以新定义为切入点,融合了向量的减法,解题的关键是正确理解新定义.

练习册系列答案
相关题目
 点
点 在
在 上的射影为点
上的射影为点 ,则
,则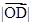 的最大值为 .
的最大值为 . 为抛物线
为抛物线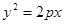 (
(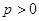 )的焦点,
)的焦点,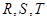 为该抛物线上三点,若
为该抛物线上三点,若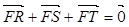 ,且
,且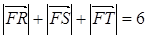
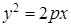 的方程;
的方程; 点的坐标为(
点的坐标为( ,
, )其中
)其中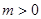 ,过点F作斜率为
,过点F作斜率为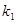 的直线与抛物线交于
的直线与抛物线交于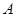 、
、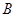 两点,
两点,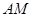 、
、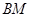 并延长交抛物线于
并延长交抛物线于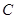 、
、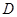 两点,设直线
两点,设直线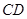 的斜率为
的斜率为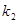 .若
.若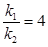 ,求
,求 ,则△AOC与△ABC的面积的比值为 ( )
,则△AOC与△ABC的面积的比值为 ( )


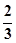
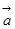 ,
,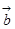 满足
满足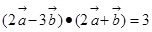 。
。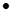
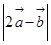 的值。
的值。 内部一点,
内部一点,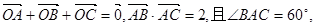 则
则 的面积为( )
的面积为( ) 


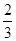
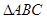 中,点
中,点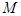 是
是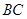 的中点,点
的中点,点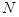 在
在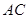 上,且
上,且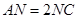 ,
,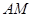 与
与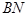 交于点
交于点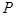 ,求
,求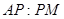 与
与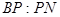 的值。
的值。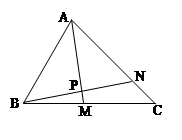
 则
则 方向上的投影为
方向上的投影为 ;
; 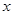 的不等式
的不等式 恒成立,则
恒成立,则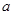 的取值范围是
的取值范围是 ;
; 为奇函数的充要条件是
为奇函数的充要条件是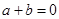 ;
;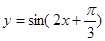 图像向右平移
图像向右平移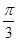 个单位,得到函数
个单位,得到函数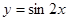 的图像
的图像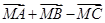 等于( )
等于( )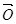 B.
B.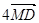 C.
C. 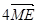 D.
D.