题目内容
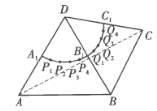
【题目】如图，正四面体
的各棱长均为2，
、
、
分别为棱
、
、
的中点，以
为圆心、1为半径，分别在面
、面
内作弧
，并将两弧各分成五等份，分点顺次为、
、
、
、
、以及、
、
、
、
、.一只甲虫欲从点出发，沿四面体表面爬行至点，则其爬行的最短距离为___________。
【答案】
【解析】
作两种展开，然后比较.
注意到弧
被点
、
、
、
分成五段等弧，每段弧对应的中心角各为
；
弧
被
、
、
、
分成五段等弧，每段弧对应的中心角也各为.
若将
绕线段
旋转，使之与
共面，
这两段弧均与圆心为
、半径为1的圆周重合，
则弧
对应的圆心角为
，此时，点、之间的直线距离为
.
若将绕线段
旋转，绕线段
旋转，使之均与
共面，
在所得图形中，弧对应的圆心角为
，
此时，点、之间的直线距离为.
综上，所求最短距离为.
练习册系列答案
相关题目
