题目内容
【题目】如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.
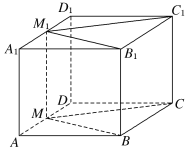
(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠BMC=∠B1M1C1.
【答案】(1)证明详见解析;(2)证明详见解析.
【解析】
(1)利用正方体的性质,根据平行四边形的定义与性质证明即可;(2)根据正方体的性质以及平行四边形的性质可证明![]() ,从而可得结果.
,从而可得结果.
(1)在正方形ADD1A1中,M、M1分别为AD、A1D1的中点,
∴MM1∥AA1,MM1=AA1.
又∵AA1∥BB1,AA1=BB1,
∴MM1∥BB1,且MM1=BB1,
∴四边形BB1M1M为平行四边形.
(2)法一:由(1)知四边形BB1M1M为平行四边形,
∴B1M1∥BM.同理可得四边形CC1M1M为平行四边形,
∴C1M1∥CM.
由平面几何知识可知,∠BMC和∠B1M1C1都是锐角.
∴∠BMC=∠B1M1C1.
法二:由(1)知四边形BB1M1M为平行四边形,
∴B1M1=BM.
同理可得四边形CC1M1M为平行四边形,
∴C1M1=CM.
又∵B1C1=BC,∴△BCM≌△B1C1M1.
∴∠BMC=∠B1M1C1.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目