题目内容
【题目】已知定义在R上的可导函数f (x)的导函数为
，满足＜f (x)，且f (x＋2)为偶函数，f (4)＝1，则不等式f (x)＜ex的解集为________．
【答案】
【解析】
令
，利用导数和已知即可得出其单调性．再利用函数的奇偶性和已知可得g（0）＝1，即可得出．
令，
则
，
∵f′（x）＜f（x），∴g′（x）＜0．
∴g（x）在R上单调递减．
∵函数f（x+2）是偶函数，
∴函数f（﹣x+2）＝f（x+2），
∴函数关于x＝2对称，
∴f（0）＝f（4）＝1，
原不等式等价为g（x）＜1，
∵g（0）
1．
∴g（x）＜1g（x）＜g（0），
∵g（x）在R上单调递减，
∴x＞0．
∴不等式f（x）＜ex的解集为（0，+∞）．
故答案为：（0，+∞）．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
【题目】某商店为了解气温对某产品销售量的影响，随机记录了该商店
月份中
天的日销售量
（单位：千克）与该地当日最低气温
（单位：℃）的数据，如表所示：
|
|
|
|
|
|
|
|
|
|
|
|
（1）求与的回归方程
：
（2）判断与之间是正相关还是负相关；若该地月份某天的最低气温为
，请用（1）中的回归方程预测该商店当日的销售量．
参考公式：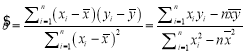
，
．
