题目内容
【题目】如图1,ABCD为菱形,∠ABC=60°,△PAB是边长为2的等边三角形,点M为AB的中点,将△PAB沿AB边折起,使平面PAB⊥平面ABCD,连接PC、PD,如图2,
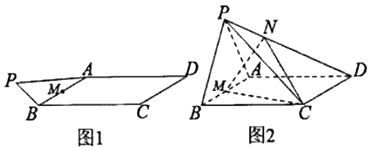
(1)证明:AB⊥PC;
(2)求PD与平面ABCD所成角的正弦值
(3)在线段PD上是否存在点N,使得PB∥平面MC?若存在,请找出N点的位置;若不存在,请说明理由
【答案】(1)证明见解析 (2)![]() .(3)存在,PN
.(3)存在,PN![]() .
.
【解析】
(1)只需证明AB⊥面PMC,即可证明AB⊥PC;
(2)由PM⊥面ABCD得∠PDM为PD与平面ABCD所成角,解△PDM即可求得PD与平面ABCD所成角的正弦值.
(3)设DB∩MC=E,连接NE,可得PB∥NE,![]() .即可.
.即可.
(1)证明:∵△PAB是边长为2的等边三角形,点M为AB的中点,
∴PM⊥AB.
∵ABCD为菱形,∠ABC=60°.∴CM⊥AB,且PM∩MC=M,
∴AB⊥面PMC,
∵PC面PMC,∴AB⊥PC;
(2)∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,PM⊥AB.
∴PM⊥面ABCD,
∴∠PDM为PD与平面ABCD所成角.
PM![]() ,MD
,MD![]() ,PD
,PD![]()
sin∠PMD![]() ,
,
即PD与平面ABCD所成角的正弦值为![]() .
.
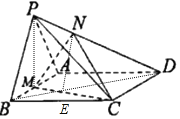
(3)设DB∩MC=E,连接NE,
则有面PBD∩面MNC=NE,
∵PB∥平面MNC,∴PB∥NE.
∴![]() .
.
线段PD上存在点N,使得PB∥平面MNC,且PN![]() .
.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
