题目内容
【题目】某营养协会对全市18岁男生的身高作调查,统计显示全市18岁男生的身高服从正态分布![]() ,现某校随机抽取了100名18岁男生的身高分析,结果这100名学生的身高全部介于
,现某校随机抽取了100名18岁男生的身高分析,结果这100名学生的身高全部介于![]() 到
到![]() 之间.现将结果按如下方式分为6组,第一组
之间.现将结果按如下方式分为6组,第一组![]() ,第二组
,第二组![]() ,…,第六组
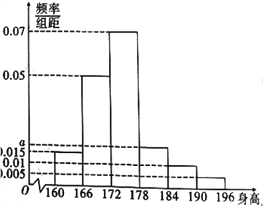
,…,第六组![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
(1)若全市18岁男生共有![]() 人,试估计该市身高在
人,试估计该市身高在![]() 以上的18岁男生人数;
以上的18岁男生人数;
(2)求![]() 的值,并计算该校18岁男生的身高的中位数(精确到小数点后三位);
的值,并计算该校18岁男生的身高的中位数(精确到小数点后三位);
(3)若身高![]() 以上的学生校服需要单独定制,现从这100名学生中身高在
以上的学生校服需要单独定制,现从这100名学生中身高在![]() 以上的同学中任意抽取3人,这三人中校服需要单独定制的人数记为
以上的同学中任意抽取3人,这三人中校服需要单独定制的人数记为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附: ![]() ,则
,则![]() ;
;
![]() ,则
,则![]() ;
;
![]() ,则
,则![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)分布列见解析,
;(3)分布列见解析, ![]() .
.
【解析】试题分析:
(1)根据正态分布得到![]() ,故
,故![]() ,从而可得身高在
,从而可得身高在![]() 以上的18岁男生人数.(2)根据频率分布直方图中所有小长方形的面积和为1可求得
以上的18岁男生人数.(2)根据频率分布直方图中所有小长方形的面积和为1可求得![]() ,然后根据中位数的意义可求得中位数的估计值.(3)由频率分布直方图可得身高在
,然后根据中位数的意义可求得中位数的估计值.(3)由频率分布直方图可得身高在![]() 内的为
内的为![]() 人,身高在
人,身高在![]() 内的为
内的为![]() 人.从而可得随机变量
人.从而可得随机变量![]() 的所有可能取值,并根据古典概型求得对应的概率,于是可得分布列,从而可得期望.
的所有可能取值,并根据古典概型求得对应的概率,于是可得分布列,从而可得期望.
试题解析:
(1)由题意得![]() ,
,
∴![]() ,
,
∴可估计该市身高在![]() 以上的18岁男生人数为
以上的18岁男生人数为![]() (人)
(人)
(2)由频率分布直方图可得![]() ,
,
∴![]() .
.
设中位数为![]() ,则
,则![]() ,
,
∴![]() .
.
即中位数为![]() .
.
(3)由题意得身高在![]() 内的人数为
内的人数为![]() 人,
人,
身高在![]() 内的人数为
内的人数为![]() 人,
人,
由题意得随机变量![]() 的所有可能取值为0,1,2,3.
的所有可能取值为0,1,2,3.
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
故![]() 的分布列如下:
的分布列如下:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
∴![]() .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目