题目内容
【题目】盒中共有9个球,其中有4个红球、3个黄球和2个绿球,这些球除颜色外完全相同.
(1)从盒中一次随机取出2个球,求取出的2个球的颜色相同的概率P;
(2)从盒中一次随机取出4个球,其中红球、黄球、绿球的个数分别记为x1,x2,x3,随机变量X表示x1,x2,x3中的最大数,求X的概率分布和数学期望E(X).
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)先求出取2个球的所有可能,再求出颜色相同的所有可能,最后利用概率公式计算即可;
(2)先判断![]() 的所有可能值,在分别求出所有可能值的概率,列出分布列,根据数学期望公式计算即可.
的所有可能值,在分别求出所有可能值的概率,列出分布列,根据数学期望公式计算即可.
试题解析:(1)取到的2个颜色相同的球可能是2个红球、2个黄球或2个绿球,
所以P=![]() =
=![]() =
=![]() .
.
(2)随机变量X所有可能的取值为2,3,4.
{X=4}表示的随机事件是“取到的4个球是4个红球”,故P(X=4)=![]() =
=![]() ;
;
{X=3}表示的随机事件是“取到的4个球是3个红球和1个其他颜色的球,或3个黄球和1个其他颜色的球”,
故P(X=3)=![]() =
=![]() =
=![]() ;
;
于是P(X=2)=1-P(X=3)-P(X=4)
=1-![]() -
-![]() =
=![]() .
.
所以随机变量X的概率分布如下表:
X | 2 | 3 | 4 |
P |
|
|
|
因此随机变量X的数学期望
E(X)=2×![]() +3×
+3×![]() +4×
+4×![]() =
=![]() .
.

 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】节能灯的质量通过其正常使用时间来衡量,使用时间越长,表明质量越好,且使用时间大于或等于6千小时的产品为优质品.现用A,B两种不同型号的节能灯做试验,各随机抽取部分产品作为样本,得到试验结果的频率分布直方图如图所示.
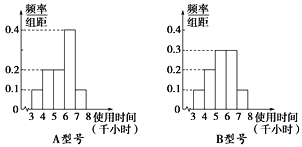
以上述试验结果中使用时间落入各组的频率作为相应的概率.
(1)现从大量的A,B两种型号节能灯中各随机抽取两件产品,求恰有两件是优质品的概率;
(2)已知A型节能灯的生产厂家对使用时间小于6千小时的节能灯实行“三包”.通过多年统计发现,A型节能灯每件产品的利润y(单位:元)与其使用时间t(单位:千小时)的关系如下表:
使用时间t(单位:千小时) | t<4 | 4≤t<6 | t≥6 |
每件产品的利润y(单位:元) | -10 | 10 | 20 |
若从大量的A型节能灯中随机抽取两件,其利润之和记为X(单位:元),求X的分布列及数学期望.