题目内容
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行.函数
轴平行.函数![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求证:函数![]() 共有两个零点,一个零点是
共有两个零点,一个零点是![]() ,另一个零点
,另一个零点![]() 在区间
在区间![]() 内;
内;
(Ⅲ)求证:存在![]() ,当
,当![]() 时,
时, ![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() ;(Ⅲ)见解析.
;(Ⅲ)见解析.
【解析】试题分析:
(Ⅰ)由题意可得![]() ,利用导函数研究函数的切线可知
,利用导函数研究函数的切线可知![]() ,则
,则![]() .
.
(Ⅱ)由题意可得![]() ,且
,且![]() ,
, ![]() ,
, ![]() ,据此可得
,据此可得![]() 存在两个零点,且一个零点为
存在两个零点,且一个零点为![]() ,第二个零点在区间
,第二个零点在区间![]() 内.
内.
(Ⅲ)由题意可得![]() ,结合(Ⅱ)的结论可知函数在
,结合(Ⅱ)的结论可知函数在![]() 上单调递增,且
上单调递增,且![]() ,则函数在
,则函数在![]() 上单调递增,则存在
上单调递增,则存在![]() ,当
,当![]() 时,
时, ![]() .
.
试题解析:
(Ⅰ)![]() ,
,
![]() ,解得
,解得![]() .
.
(Ⅱ)![]() ,令
,令![]() 得到
得到![]() .
.
|
|
|
|
|
|
|
|
|
| 极小值 |
|
![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() 存在两个零点,且一个零点为
存在两个零点,且一个零点为![]() ,
,
![]() ,
, ![]() ,
, ![]() 所以第二个零点在区间
所以第二个零点在区间![]() 内.
内.
(Ⅲ)证明: ![]() ,
, ![]()
令![]() 可得
可得![]()
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
而![]() ,函数在
,函数在![]() 上单调递增,
上单调递增,
所以当![]() ,
, ![]() 恒成立,
恒成立,
所以存在![]() ,当
,当![]() 时,
时, ![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】节能灯的质量通过其正常使用时间来衡量,使用时间越长,表明质量越好,且使用时间大于或等于6千小时的产品为优质品.现用A,B两种不同型号的节能灯做试验,各随机抽取部分产品作为样本,得到试验结果的频率分布直方图如图所示.
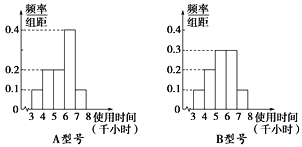
以上述试验结果中使用时间落入各组的频率作为相应的概率.
(1)现从大量的A,B两种型号节能灯中各随机抽取两件产品,求恰有两件是优质品的概率;
(2)已知A型节能灯的生产厂家对使用时间小于6千小时的节能灯实行“三包”.通过多年统计发现,A型节能灯每件产品的利润y(单位:元)与其使用时间t(单位:千小时)的关系如下表:
使用时间t(单位:千小时) | t<4 | 4≤t<6 | t≥6 |
每件产品的利润y(单位:元) | -10 | 10 | 20 |
若从大量的A型节能灯中随机抽取两件,其利润之和记为X(单位:元),求X的分布列及数学期望.