题目内容
已知全集U=R,A,B为其子集,若集合A={y|y=log3x,x>3},B={y|y=(
)x,x≥1},则(∁UA)∩B等于( )
| 1 |
| 2 |
A、{y|y≤
| ||
B、{y|0<y≤
| ||
C、{y|
| ||
| D、∅ |
考点:交、并、补集的混合运算
专题:函数的性质及应用,集合
分析:根据对数函数、指数函数的单调性求出集合A、B,再由补集、交集的运算求出∁UA和(∁UA)∩B.
解答:
解:因为函数y=(
)x在定义域上递减,且x≥1,
所以0<y≤
,则集合B={y|0<y≤
},
因为函数y=log3x在定义域上递增,且x>3,
所以y>1,则集合A={y|y>1},
又全集U=R,则∁UA={y|y≤1},
所以(∁UA)∩B={y|0<y≤
},
故选:B.
| 1 |
| 2 |
所以0<y≤
| 1 |
| 2 |
| 1 |
| 2 |
因为函数y=log3x在定义域上递增,且x>3,
所以y>1,则集合A={y|y>1},
又全集U=R,则∁UA={y|y≤1},
所以(∁UA)∩B={y|0<y≤
| 1 |
| 2 |
故选:B.
点评:本题考查交、并、补集的混合运算,以及对数、指数函数的单调性,属于基础题.

练习册系列答案
相关题目
已知sin(π-α)=-
,且α是第四象限的角,那么cosα的值是( )
| 3 |
| 5 |
A、-
| ||
B、
| ||
C、±
| ||
D、
|
若p:?x∈R,sinx≤1,则( )
| A、?p:?x∈R,sinx>1 |
| B、?p:?x∈R,sinx>1 |
| C、?p:?x∈R,sinx≥1 |
| D、?p:?x∈R,sinx≥1 |
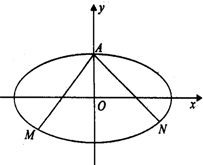 如图已知椭圆
如图已知椭圆