题目内容
已知函数f(x)=
(x∈R)
(1)判断函数f(x)的奇偶性;
(2)若对任意的x∈R,都有不等式f(2x)+f(x2-m)>0恒成立,求实数m的取值范围.
| 2x-1 |
| 2x+1 |
(1)判断函数f(x)的奇偶性;
(2)若对任意的x∈R,都有不等式f(2x)+f(x2-m)>0恒成立,求实数m的取值范围.
考点:函数恒成立问题,函数奇偶性的性质
专题:综合题,函数的性质及应用
分析:(1)利用奇函数的定义,即可判断函数f(x)的奇偶性;
(2)f(x)=
=1-
在R上递增,且为奇函数,可得x2+2x-m>0,对任意的x∈R恒成立,运用判别式小于0,即可得到m的范围.
(2)f(x)=
| 2x-1 |
| 2x+1 |
| 2 |
| 2x+1 |
解答:
解:(1)∵f(-x)=
=-
=-f(x),
∴f(x)为奇函数;
(2)∵f(x)=
=1-
在R上递增,且为奇函数
∴f(x2-m)>f(-2x),
∴x2-m>-2x
即x2+2x-m>0,对任意的x∈R恒成立,
则判别式△=4+4m<0,解得m<-1.
| 2-x-1 |
| 2-x+1 |
| 2x-1 |
| 2x+1 |
∴f(x)为奇函数;
(2)∵f(x)=
| 2x-1 |
| 2x+1 |
| 2 |
| 2x+1 |
∴f(x2-m)>f(-2x),
∴x2-m>-2x
即x2+2x-m>0,对任意的x∈R恒成立,
则判别式△=4+4m<0,解得m<-1.
点评:本题考查函数的奇偶性和单调性及运用,考查二次不等式恒成立问题,注意运用判别式小于0,属于中档题.

练习册系列答案
相关题目
在等差数列{an}中,若a4+a8+a12=12,则2a9-a10的值是( )
| A、3 | B、4 | C、6 | D、8 |
已知全集U=R,A,B为其子集,若集合A={y|y=log3x,x>3},B={y|y=(
)x,x≥1},则(∁UA)∩B等于( )
| 1 |
| 2 |
A、{y|y≤
| ||
B、{y|0<y≤
| ||
C、{y|
| ||
| D、∅ |
对一切实数x,当a<b时,二次函数f(x)=ax2+bx+c的值恒为非负数,则b-2a-
的最大值为( )
| c |
| 2 |
| A、0 | B、1 | C、2 | D、-1 |
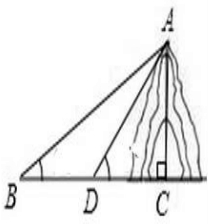 如图,从B处看山顶A的仰角为45°,向前100米,在D处看山顶A的仰角为60°,求:山AC的高度(已知sin15°=
如图,从B处看山顶A的仰角为45°,向前100米,在D处看山顶A的仰角为60°,求:山AC的高度(已知sin15°=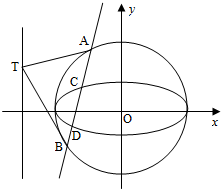 已知椭圆C1的中心在坐标原点,焦点在x轴上,且经过点
已知椭圆C1的中心在坐标原点,焦点在x轴上,且经过点