题目内容
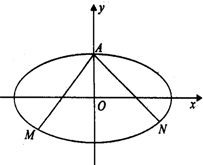如图已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
（1）求椭圆的方程；
（2）过点A作两条互相垂直的直线分别交椭圆于M，N两点．求证：直线恒过定点P．并求点P的坐标．
考点：直线与圆锥曲线的综合问题
专题：综合题,圆锥曲线的定义、性质与方程
分析：（1）根据椭圆
+
=1（a＞b＞0）的离心率为
，且过点A（0，1），求出a，b，即可求椭圆的方程；
（2）设直线l1的方程为y=kx+1，联立椭圆方程，求出M，N的坐标，可得kMP=
=
，kNP=
=
，kMP=kNP．即可证明结论．
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
（2）设直线l1的方程为y=kx+1，联立椭圆方程，求出M，N的坐标，可得kMP=
yM+
| ||
| xM |
| k2-1 |
| 5k |
yN+
| ||
| xN |
| k2-1 |
| 5k |
解答：
解：（1）因为椭圆
+
=1（a＞b＞0）的离心率为
，且过点A（0，1）．
所以b=1，
=
，
所以a=2，b=1
所以椭圆C的方程为：
+y2=1…（3分）
（2）直线MN恒过定点P（0，-
)，下面给予证明：
设直线l1的方程为y=kx+1，联立椭圆方程，消去y得；（4k2+1）x2+8kx=0，
解得xM=-
，yM=
同理可得：xN=
，yN=
…（8分）
kMP=
=
，kNP=
=
∴kMP=kNP．
故直线MN恒过定点P （0，-
）．…（12分）
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
所以b=1，
| c |
| a |
| ||
| 2 |
所以a=2，b=1
所以椭圆C的方程为：
| x2 |
| 4 |
（2）直线MN恒过定点P（0，-
| 3 |
| 5 |
设直线l1的方程为y=kx+1，联立椭圆方程，消去y得；（4k2+1）x2+8kx=0，
解得xM=-
| 8k |
| 4k2+1 |
| 1-4k2 |
| 4k2+1 |
同理可得：xN=
| 8k |
| k2+4 |
| k2-4 |
| k2+4 |
kMP=
yM+
| ||
| xM |
| k2-1 |
| 5k |
yN+
| ||
| xN |
| k2-1 |
| 5k |
∴kMP=kNP．
故直线MN恒过定点P （0，-
| 3 |
| 5 |
点评：本题考查椭圆的方程，考查直线与椭圆的位置关系，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
字词句段篇系列答案
相关题目
已知全集U=R，A，B为其子集，若集合A={y|y=log3x，x＞3}，B={y|y=(
)x，x≥1}，则（∁UA）∩B等于（ ）
| 1 |
| 2 |
A、{y|y≤
| ||
B、{y|0＜y≤
| ||
C、{y|
| ||
| D、∅ |
已知椭圆C1的中心在坐标原点，焦点在x轴上，且经过点