题目内容
【题目】在平面直角坐标系中,以原点为极点,![]() 轴非负半轴为极轴极坐标,曲线
轴非负半轴为极轴极坐标,曲线![]() 的方程:
的方程: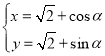 (
(![]() 为参数),曲线
为参数),曲线![]() 的方程:
的方程: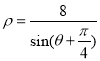 .
.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标系方程;
的直角坐标系方程;
(2)从![]() 上任意一点
上任意一点![]() 作曲线
作曲线![]() 的切线,设切点为
的切线,设切点为![]() ,求切线长
,求切线长![]() 的最小值及此时点
的最小值及此时点![]() 的极坐标.
的极坐标.
【答案】(1) 曲线C1![]() ,曲线C2 x+y﹣8
,曲线C2 x+y﹣8![]() =0; (2)|PQ|的最小值=
=0; (2)|PQ|的最小值=![]() , P极坐标为:
, P极坐标为:![]()
【解析】
(1)曲线![]() 的方程
的方程 为参数),消去参数可得:
为参数),消去参数可得:
![]() .曲线
.曲线![]() 的方程:
的方程: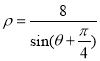 ,化为
,化为![]() ,把
,把![]() 代入即可得出.
代入即可得出.
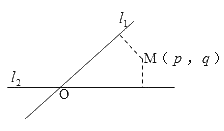
(2)如图所示,过圆心![]() 作
作![]() 直线
直线![]() ,垂足为点
,垂足为点![]() ,此时切线长
,此时切线长![]() 最小.利用点到直线的距离公式可得
最小.利用点到直线的距离公式可得![]() .
.![]() ,直线
,直线![]() 的方程为:
的方程为:![]() ,联立
,联立 ,解得
,解得![]() ,利用
,利用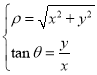 即可得出
即可得出![]() 极坐标.
极坐标.
解:(1)曲线![]() 的方程
的方程 为参数),消去参数可得:
为参数),消去参数可得:![]() .
.
曲线![]() 的方程:
的方程: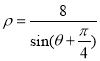 ,化为
,化为![]() ,
,![]()
(2)如图所示,过圆心![]() 作
作![]() 直线
直线![]() ,垂足为点
,垂足为点![]() ,此时切线长
,此时切线长![]() 最小.
最小.
![]() .
.
![]() ,
,
直线![]() 的方程为:
的方程为:![]() ,
,
联立 ,解得
,解得![]() .
.
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() .
.
![]() .
.


练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目