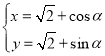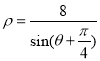题目内容
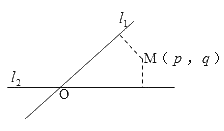
【题目】如图，平面内两条直线
和
相交于点
，构成的四个角中的锐角为
.对于平面上任意一点
，若
，
分别是到直线和的距离，则称有序非负实数对
是点的“距离坐标”，给出下列四个命题：
①
点有且仅有两个；
②
点有且仅有4个；
③若
，则点的轨迹是两条过点的直线；
④满足
的所有点位于一个圆周上.
其中正确命题的个数是（ ）
A.1B.2C.3D.4
【答案】C
【解析】
通过画图分析依次判断每个命题的真假，尤其是第四个命题，可举出反例判断其错误即可.
命题①，如图，有且只有两个点的距离坐标为
，即命题①正确.
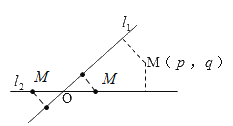
命题②，如图，虚线分别为到两条直线的距离为2和3的平行直线，四条虚线总共4个交点，故
点有且仅有4个，即命题②正确；
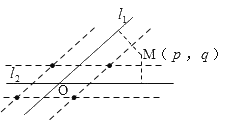
命题③，如图，点
的轨迹是两条过
点的直线l3和l4，即命题③正确；
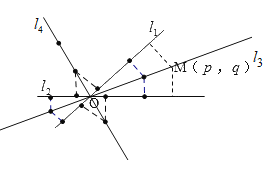
命题④，如图，
和
分别在直线l1和l2上，
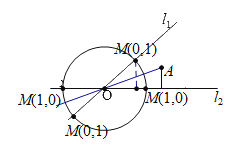
易得
，则点M都在以O为圆心，半径为
的圆上，
设点
，即点A到两条直线的距离都是
，且满足
，
由几何关系可得，
，即点A在圆O外，故命题④错误.
综上，正确命题为①②③.
故选：C.
练习册系列答案
名校课堂系列答案
相关题目
