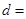题目内容
设数列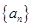 的前
的前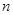 项和为
项和为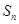 ,已知
,已知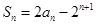 (n∈N*).
(n∈N*).
(1)求数列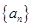 的通项公式;
的通项公式;
(2)设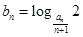 ,数列
,数列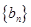 的前
的前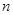 项和为
项和为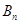 ,若存在整数
,若存在整数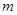 ,使对任意n∈N*且n ≥2,都有
,使对任意n∈N*且n ≥2,都有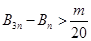 成立,求
成立,求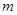 的最大值;
的最大值;
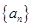 的前
的前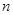 项和为
项和为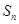 ,已知
,已知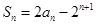 (n∈N*).
(n∈N*).(1)求数列
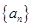 的通项公式;
的通项公式;(2)设
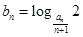 ,数列
,数列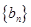 的前
的前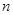 项和为
项和为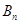 ,若存在整数
,若存在整数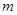 ,使对任意n∈N*且n ≥2,都有
,使对任意n∈N*且n ≥2,都有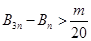 成立,求
成立,求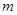 的最大值;
的最大值;(1)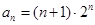 . (2)
. (2)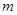 的最大值为18.
的最大值为18.
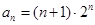 . (2)
. (2)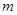 的最大值为18.
的最大值为18. (1)本小题是由an的前n项和求通项的典型题目.可以用n-1替换式子当中的n,得到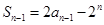 ,然后两式作差可求得an与an-1的递推关系
,然后两式作差可求得an与an-1的递推关系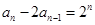 ,然后再通过两边同除
,然后再通过两边同除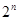 ,可确定数列
,可确定数列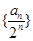 是等差数列.问题到此得以解决.
是等差数列.问题到此得以解决.
(2)先求出 ,则
,则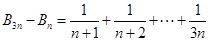 ,然后再令
,然后再令 ,研究其单调性,确定其最小值,使其最小值大于
,研究其单调性,确定其最小值,使其最小值大于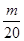 即可.s
即可.s
(1)由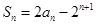 ,得
,得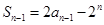 (n≥2).
(n≥2).
两式相减,得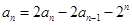 ,即
,即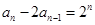 (n≥2).
(n≥2).
于是 ,所以数列
,所以数列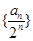 是公差为1的等差数列.又
是公差为1的等差数列.又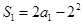 ,所以
,所以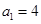 .
.
所以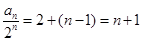 ,故
,故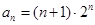 . 7分
. 7分
(2)因为
 ,则
,则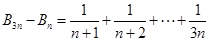
令 ,则
,则
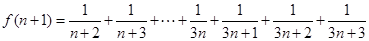 .
.
所以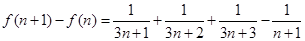
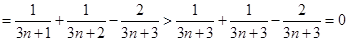 .
.
即 ,所以数列
,所以数列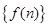 为递增数列.
为递增数列.
所以当n ≥2时, 的最小值为
的最小值为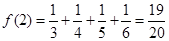 .
.
据题意, ,即
,即 .又
.又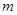 为整数,故
为整数,故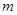 的最大值为18.
的最大值为18.
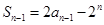 ,然后两式作差可求得an与an-1的递推关系
,然后两式作差可求得an与an-1的递推关系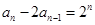 ,然后再通过两边同除
,然后再通过两边同除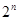 ,可确定数列
,可确定数列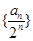 是等差数列.问题到此得以解决.
是等差数列.问题到此得以解决.(2)先求出
 ,则
,则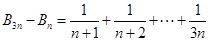 ,然后再令
,然后再令 ,研究其单调性,确定其最小值,使其最小值大于
,研究其单调性,确定其最小值,使其最小值大于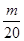 即可.s
即可.s(1)由
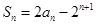 ,得
,得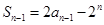 (n≥2).
(n≥2).两式相减,得
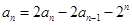 ,即
,即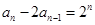 (n≥2).
(n≥2). 于是
 ,所以数列
,所以数列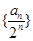 是公差为1的等差数列.又
是公差为1的等差数列.又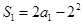 ,所以
,所以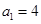 .
. 所以
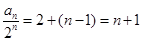 ,故
,故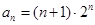 . 7分
. 7分(2)因为

 ,则
,则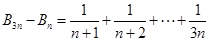
令
 ,则
,则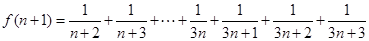 .
.所以
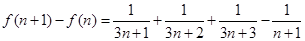
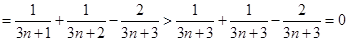 .
.即
 ,所以数列
,所以数列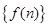 为递增数列.
为递增数列.所以当n ≥2时,
 的最小值为
的最小值为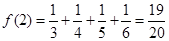 .
.据题意,
 ,即
,即 .又
.又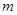 为整数,故
为整数,故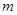 的最大值为18.
的最大值为18.
练习册系列答案
相关题目
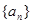 的首项
的首项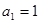 ,前
,前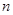 项和
项和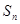 满足
满足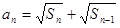
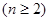 .
.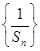 的前
的前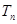 ,求证:
,求证: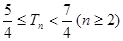 .
.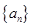 的前n项和为Sn ,且满足
的前n项和为Sn ,且满足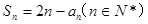 。
。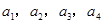 ;
;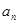 ,并用数学归纳法证明。
,并用数学归纳法证明。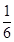 , 前n项和Sn=
, 前n项和Sn=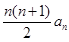 ,
,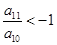 ,且它们的前n项和为Sn有最大值,则使得Sn<0的n的最小值为( )
,且它们的前n项和为Sn有最大值,则使得Sn<0的n的最小值为( )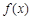 对任意
对任意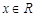 都有
都有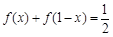 .
.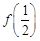 和
和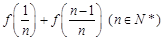 的值;
的值;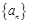 满足:
满足: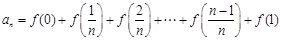 ,数列{an}是等差数列吗?请给予证明;
,数列{an}是等差数列吗?请给予证明;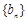 满足
满足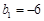 ,
,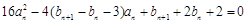 ,试求数列
,试求数列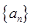 中,
中,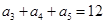 ,那么
,那么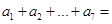 .
.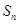 是公差不为零的等差数列
是公差不为零的等差数列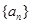 的前n项和,若
的前n项和,若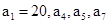 成等比数列,则
成等比数列,则
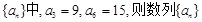 的公差
的公差