Question

【题目】已知函数为偶函数，函数为奇函数。对任意实数x恒成立.

（1）求函数与；

（2）设，，若对于恒成立，求实数m的取值范围；

（3）对于（2）中的函数，若方程没有实数解，实数m的取值范围.

Answer 1

【答案】（1），（2）（3）.

【解析】

（1）利用函数的奇偶性，列方程组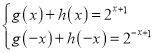求函数的解析式；

（2）由（1）变形，由不等式 恒成立，，参变分离后恒成立，转化为求函数的最大值；

（3）首先讨论解得情况，当时，满足条件，当时，方程有两个根，，假设，由于函数开口向上，故没有实数解，而的最小值为，列等价的不等式组求解，当时， ， ，时，，而无解，满足条件，综上以上三种情况求得的取值范围.

（1） ，

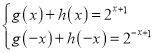函数为偶函数，函数为奇函数

即 ，两式相加得

，

；

（2）

，

，

不等式等价于 恒成立，

参变分离后恒成立，

当时，是单调递减函数，

时，函数取得最大值-3，

即；

（3）首先讨论解得情况， ，

当时，

解得：，

即当时，不管为何值时，无解，即也无解；

当时，方程有两个根，，假设，由于函数开口向上，故没有实数解，

而

函数的最小值为，故方程的大根小于，即

故有，

当时， ， ，时，，而无解，满足条件，

综上所述。