题目内容
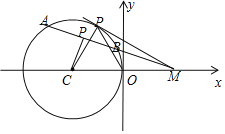
【题目】已知点M(2,0),圆C:x2+y2+4x=0.
(1)求直线3x+4y+1=0与圆C:x2+y2+4x=0相交所得的弦长|MN|;
(2)过点M的直线与圆C交于A,B两个不同的点,求弦AB的中点P的轨迹方程.
【答案】(1)2![]() ;(2)x2+y2=4,(x<﹣1).
;(2)x2+y2=4,(x<﹣1).
【解析】
(1)将圆的方程转化为标准形式,求出圆心与半径,再利用点到直线的距离公式求出圆心到直线的距离,从而可求出弦长|MN|=2![]() 2
2![]() .
.
(2)当M与P不重合时,连结CP,则CP⊥MP,从而可得|CP|2+|MP|2=|CM|2,设P(x,y),利用两点间的距离公式列方程即可求解.
(1)圆C:x2+y2+4x=0
可得圆C:(x+2)2+y2=4,圆心坐标(﹣2,0)半径为2,
圆的圆心到直线的距离为:d![]() 1,
1,
∴直线3x+4y+1=0与圆C:x2+y2+4x=0相交所得的弦长|MN|=2![]() 2
2![]() ;
;
(2)解:当M与P不重合时,连结CP,则CP⊥MP,
∴|CP|2+|MP|2=|CM|2,
设P(x,y),则(x+2)2+y2+(x﹣2)2+y2=16,
化简得:x2+y2=4(x<﹣1),
故弦AB中点P的轨迹方程是x2+y2=4,(x<﹣1).

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目