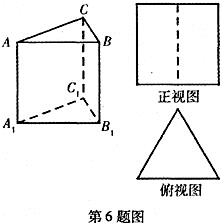
题目内容
如图,在长方体 中,已知
中,已知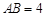 ,
,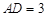 ,
,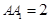 ,E,F分别是棱AB,BC 上的点,且
,E,F分别是棱AB,BC 上的点,且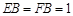 .
.

(1)求异面直线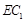 与
与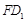 所成角的余弦值;
所成角的余弦值;
(2)试在面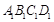 上确定一点G,使
上确定一点G,使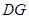
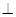 平面
平面 .
.
 中,已知
中,已知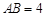 ,
,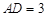 ,
,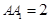 ,E,F分别是棱AB,BC 上的点,且
,E,F分别是棱AB,BC 上的点,且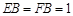 .
.
(1)求异面直线
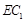 与
与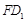 所成角的余弦值;
所成角的余弦值;(2)试在面
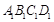 上确定一点G,使
上确定一点G,使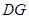
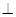 平面
平面 .
.(1)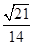
(2)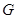 在面
在面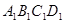 上,且到
上,且到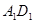 ,
,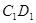 距离均为
距离均为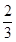 时,
时,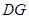
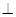 平面
平面 .
.
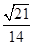
(2)
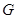 在面
在面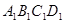 上,且到
上,且到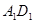 ,
,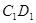 距离均为
距离均为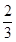 时,
时,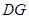
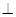 平面
平面 .
.(1)先建立空间直角坐标系,然后把异面直线的夹角问题转化为两直线所在向量的夹角问题;(2)利用待定系数法的思想设出点的坐标,利用直线与面垂直转化为两向量垂直,再结合数量积知识列出坐标方程求得点的坐标,最后确定点的位置
解:(1)以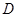 为原点,
为原点,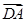 ,
,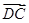 ,
,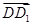 分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有
分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有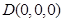 ,
,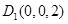 ,
,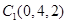 ,
,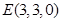 ,
,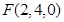 ,
,

于是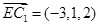 ,
,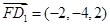 .
.
设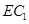 与
与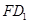 所成角为
所成角为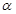 ,则
,则
 .
.
∴异面直线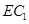 与
与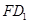 所成角的余弦值为
所成角的余弦值为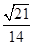 .
.
(2)因点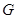 在平面
在平面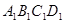 上,故可设
上,故可设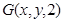 .
.
 ,
,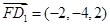 ,
,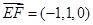 .
.
由 得
得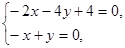 解得
解得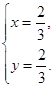
故当点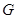 在面
在面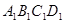 上,且到
上,且到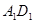 ,
,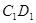 距离均为
距离均为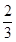 时,
时,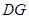
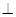 平面
平面 .
.
解:(1)以
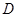 为原点,
为原点,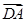 ,
,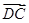 ,
,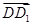 分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有
分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有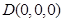 ,
,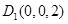 ,
,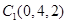 ,
,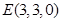 ,
,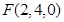 ,
,
于是
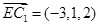 ,
,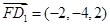 .
.设
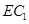 与
与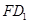 所成角为
所成角为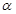 ,则
,则 .
.∴异面直线
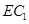 与
与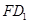 所成角的余弦值为
所成角的余弦值为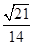 .
.(2)因点
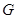 在平面
在平面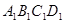 上,故可设
上,故可设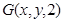 .
. ,
,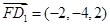 ,
,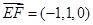 .
.由
 得
得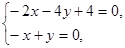 解得
解得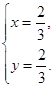
故当点
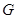 在面
在面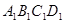 上,且到
上,且到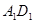 ,
,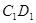 距离均为
距离均为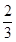 时,
时,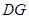
 平面
平面 .
.
练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目


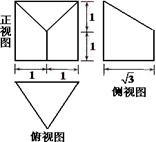

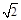 .将
.将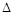 ABD沿矩形的对角线BD所在的直线进行翻着,在翻着过程中,
ABD沿矩形的对角线BD所在的直线进行翻着,在翻着过程中,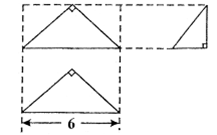
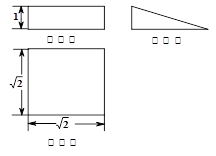
 a2
a2 a2
a2 a2
a2