题目内容
10. 如图,在等腰梯形ABDE中,AE=ED=BD=a,当等腰梯形ABDE的面积最大时,角θ为( )
如图,在等腰梯形ABDE中,AE=ED=BD=a,当等腰梯形ABDE的面积最大时,角θ为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{8}$ |
分析 由题意可得面积的表达式,求导数解方程可得.
解答 解:由题意可得等腰梯形ABDE的面积S=a2(1+cosθ)sinθ,
即f(x)=(1+cosx)sinx,x∈(0,$\frac{π}{2}$)
求导数可得f′(x)=(1+cosx)′sinx+(1+cosx)(sinx)′
=-sin2x+(1+cosx)cosx=2cos2x+cosx-1=0,
解得cosx=$\frac{1}{2}$,或cosx=-1(舍去)
故当角θ为$\frac{θ}{3}$时,原式取到最大值
故选:B.
点评 本题考查三角函数的最值,涉及导数的应用和二次方程的求解,属中档题.

练习册系列答案
相关题目
20.已知f(x)=log2(x2-ax+3a)在[2,+∞)上是增函数,则实数a的取值范围是( )
| A. | (-∞,4) | B. | (-4,4] | C. | (-∞,-4)∪[2,+∞) | D. | [-4,4) |
5.有这样一段演绎推理:“有些整数是自然数,-2是整数,则-2是自然数”,这个结论显然是错误的,是因为( )
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 非以上错误 |
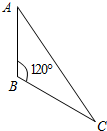 在△ABC中,AB=BC=4,∠ABC=120°,若把△ABC绕直线AB旋转一周,
在△ABC中,AB=BC=4,∠ABC=120°,若把△ABC绕直线AB旋转一周,