题目内容
2.在△ABC中,角A、B、C所对应的边分别为a、b、c,$\frac{c-a}{b-a}$=$\frac{sinB}{sinA+sinC}$.(1)求角C的大小;
(2)求函数f(x)=cos2(x+C)-sin2(x-C)的单调递增区间.
分析 (1)根据正弦定理和余弦定理,即可求角C的大小;
(2)求出函数f(x)的表达式,结合三角函数的单调性即可得到结论.
解答 解:(1)由$\frac{c-a}{b-a}$=$\frac{sinB}{sinA+sinC}$.得$\frac{c-a}{b-a}$=$\frac{b}{a+c}$,
即ab=a2+b2-c2,
由余弦定理得cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{1}{2}$,
在△ABC中,C=$\frac{π}{3}$.
(2)f(x)=cos2(x+C)-sin2(x-C)=cos2(x+$\frac{π}{3}$)-sin2(x-$\frac{π}{3}$)
=$\frac{1+cos(2x+\frac{2π}{3})}{2}$-$\frac{1-cos(2x-\frac{2π}{3})}{2}$=-$\frac{1}{2}$cos2x,
由2kπ≤2x≤2kπ+π,k∈Z,
得kπ≤x≤kπ+$\frac{π}{2}$,k∈Z,
故函数f(x)的递增区间为[kπ,kπ+$\frac{π}{2}$],k∈Z.
点评 本题主要考查解三角形的应用,考查三角函数的图象和性质,利用正弦定理和余弦定理是解决本题的关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
12.已知函数f(x)=aln(x+1)-x2在区间(1,2)内任取两个实数p,q,且p≠q,不等式$\frac{{f({p+1})-f({q+1})}}{p-q}<1$恒成立,则实数a的取值范围为( )
| A. | a≤15 | B. | 0<a≤15 | C. | a>6 | D. | a<-3 |
17.已知命题p:?x∈R,x-2>0,命题q:?x∈R,2x>x2,则下列说法中正确的是( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是真命题 | D. | 命题p∨(¬q)是假命题 |
12.在复平面上,复数z=a+bi(a,b∈R)与复数i(i-2)关于实轴对称,则a+b的值为( )
| A. | 1 | B. | -3 | C. | 3 | D. | 2 |
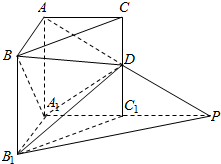 如图所示,在直三棱柱ABC-A1B1B1中,∠BAC=90°,AB=AC=AA1=1,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1.
如图所示,在直三棱柱ABC-A1B1B1中,∠BAC=90°,AB=AC=AA1=1,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1.