题目内容
【题目】已知椭圆![]() 的离心率
的离心率![]() ,一条准线方程为
,一条准线方程为![]()
⑴求椭圆![]() 的方程;
的方程;
⑵设![]() 为椭圆
为椭圆![]() 上的两个动点,
上的两个动点,![]() 为坐标原点,且
为坐标原点,且![]() .
.
①当直线![]() 的倾斜角为
的倾斜角为![]() 时,求
时,求![]() 的面积;
的面积;
②是否存在以原点![]() 为圆心的定圆,使得该定圆始终与直线
为圆心的定圆,使得该定圆始终与直线![]() 相切?若存在,请求出该定圆方程;若不存在,请说明理由.
相切?若存在,请求出该定圆方程;若不存在,请说明理由.
【答案】(1)![]() (2)①S△GOH=
(2)①S△GOH=![]() ②x2+y2=
②x2+y2=![]()
【解析】
(1)因为![]() =
=![]() ,
,![]() =
=![]() ,a2=b2+c2,
,a2=b2+c2,
解得a=3,b=![]() ,所以椭圆方程为
,所以椭圆方程为![]()
(2)①由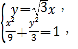 解得
解得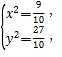 由
由 得
得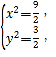
所以OG=![]() ,OH=
,OH=![]() ,所以S△GOH=
,所以S△GOH=![]() .
.
②假设存在满足条件的定圆,设圆的半径为R,则OG·OH=R·GH,
因为OG2+OH2=GH2,故![]() ,
,
当OG与OH的斜率均存在时,不妨设直线OG方程为y=kx,
由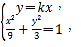 得
得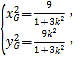 所以OG2=
所以OG2=![]() ,
,
同理可得OH2=![]() ,(将OG2中的k换成-
,(将OG2中的k换成-![]() 可得)
可得)![]() ,R=
,R=![]() ,
,
当OG与OH的斜率有一个不存在时,可得![]() ,
,
故满足条件的定圆方程为:x2+y2=![]()

练习册系列答案
相关题目