题目内容
边长为a的正三角形内任一点到三边距离之和为定值
a，类比到空间，棱长均为a的三棱锥内任一点到各面距离之和为（ ）
| ||
| 2 |
A．
| B．
| C．
| D．
|
本题可以用一个正四面体来计算一下棱长为a的三棱锥内任一点到各个面的距离之和，
如图：
由棱长为a可以得到BF=
，BO=AO=
-OE，
在直角三角形中，根据勾股定理可以得到
BO2=BE2+OE2，
把数据代入得到OE=
，
∴棱长为a的三棱锥内任一点到各个面的距离之和4×
=
故选C．
如图：
由棱长为a可以得到BF=
| ||
| 2 |
| ||
| 3 |
在直角三角形中，根据勾股定理可以得到
BO2=BE2+OE2，
把数据代入得到OE=
| ||
| 12 |
∴棱长为a的三棱锥内任一点到各个面的距离之和4×
| ||
| 12 |
| ||
| 3 |
故选C．
练习册系列答案
相关题目
，那么
，
，
中至少有一个不小于
”时，反设正确的是( )
时，比较
和
的大小并猜想（ ）
时，
时，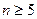
时，
时，