题目内容
14分)已知椭圆中心在原点,焦点在x轴上,一个顶点为A(0,-1),且其右焦点到直线x-y+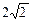 =0的距离为3.(I)求椭圆的方程;
=0的距离为3.(I)求椭圆的方程;
(II)是否存在斜率为k(k≠0)的直线l,使l与已知椭圆交于不同的两点M、N,
且|AN|=|AM|?若存在,求出k的取值范围;若不存在,请说明理由.
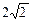 =0的距离为3.(I)求椭圆的方程;
=0的距离为3.(I)求椭圆的方程;(II)是否存在斜率为k(k≠0)的直线l,使l与已知椭圆交于不同的两点M、N,
且|AN|=|AM|?若存在,求出k的取值范围;若不存在,请说明理由.
(1)

(2)故满足条件的直线l存在,其斜率k的范围为-1<k<1且k≠0.
(I)解:由题意,设椭圆方程为: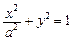 (a>1),
(a>1),
则右焦点为F (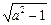 ,0),由已知
,0),由已知 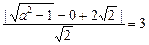 ,解得:a=
,解得:a=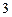
∴椭圆方程为: …………5分
…………5分
(II)解:设存在满足条件的直线l,其方程为y=kx+b(k≠0)
由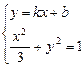 得:
得: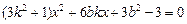 ① …………7分
① …………7分
设M(x1,y1)、N(x2,y2)是方程①的两根,则
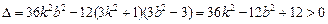 ② …………9分
② …………9分
由韦达定理得: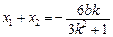
从而MN的中点P的坐标为(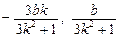 ) ……10分
) ……10分
∵|AM|=|AN| ∴AP是线段MN的垂直平分线 ∴AP⊥MN
于是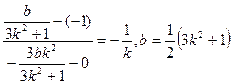 , ………12分
, ………12分
代入②并整理得:(3k2+1)(k2-1)<0,∴-1<k<1
故满足条件的直线l存在,其斜率k的范围为-1<k<1且k≠0. ………14分
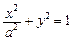 (a>1),
(a>1),则右焦点为F (
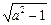 ,0),由已知
,0),由已知 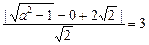 ,解得:a=
,解得:a=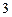
∴椭圆方程为:
 …………5分
…………5分(II)解:设存在满足条件的直线l,其方程为y=kx+b(k≠0)
由
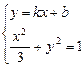 得:
得: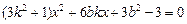 ① …………7分
① …………7分设M(x1,y1)、N(x2,y2)是方程①的两根,则
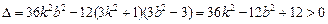 ② …………9分
② …………9分由韦达定理得:
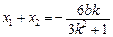
从而MN的中点P的坐标为(
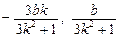 ) ……10分
) ……10分∵|AM|=|AN| ∴AP是线段MN的垂直平分线 ∴AP⊥MN
于是
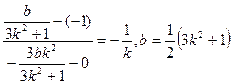 , ………12分
, ………12分代入②并整理得:(3k2+1)(k2-1)<0,∴-1<k<1
故满足条件的直线l存在,其斜率k的范围为-1<k<1且k≠0. ………14分

练习册系列答案
相关题目
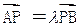 .
. ,求m的取值范围.
,求m的取值范围.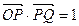 .
.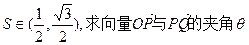 的取值范围;
的取值范围;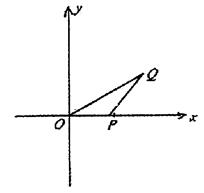
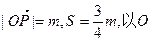 为中心,P为焦点的椭圆经过点Q,当m≥2时,求
为中心,P为焦点的椭圆经过点Q,当m≥2时,求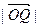 的最小值,并求出此时的椭圆方程。
的最小值,并求出此时的椭圆方程。  的取值范围。
的取值范围。
 上两点间最大的距离为8,则实数
上两点间最大的距离为8,则实数 的值是 ▲
的值是 ▲ 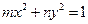 与直线
与直线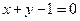 相交于
相交于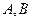 两点,过
两点,过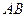 中点M与坐标原点的
中点M与坐标原点的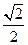 ,则
,则 的值为 ( )
的值为 ( )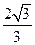
 在椭圆
在椭圆 上,若
上,若 点坐标为
点坐标为
 且
且 ,则
,则 的最小值是 .
的最小值是 .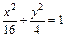 上的点到直线
上的点到直线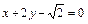 的最大距离是 ( )
的最大距离是 ( )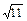


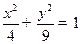 的上.下两个焦点分别为
的上.下两个焦点分别为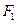 .
.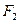 ,点
,点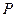 为该椭圆上一点,若
为该椭圆上一点,若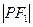 .
.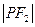 为方程
为方程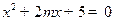 的两根,则
的两根,则 = .
= .