题目内容
【题目】已知函数![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)若![]() =0,求函数
=0,求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,证明
,证明![]() >0时,
>0时,![]() <
<![]()
【答案】(1)见解析;(2)见解析
【解析】
(1)求得![]() 的导数,讨论
的导数,讨论![]() ,
,![]() ,
,![]() ,解不等式可得所求单调区间;
,解不等式可得所求单调区间;
(2)分别求得![]() 的最大值,
的最大值,![]() 的最小值,比较即可得证.
的最小值,比较即可得证.
(1)若![]() ,则
,则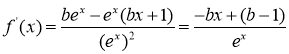 ,
,
(i)当![]() 时,
时,![]() ,函数
,函数![]() 在R上单调递减;
在R上单调递减;
(ii)当![]() 时,
时,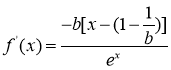 ,
,
①若![]() ,当
,当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减.
单调递减.
②若![]() ,当
,当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
综上可知,
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递减区间为R,无单调递增区间;
的单调递减区间为R,无单调递增区间;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(2)若![]() 则
则![]() ,
,![]() ,
,
要证不等式![]() ,即证
,即证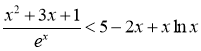 ,
,
记![]() ,则
,则![]() ,
,
故当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
所以![]() ;
;
又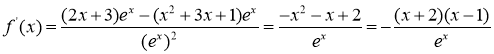 ,
,
故![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
所以![]() 时,
时,![]()
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() 时,
时,![]() .
.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案【题目】2018年1月22日,依照中国文联及中国民间文艺家协会命名中国观音文化之乡的有关规定,中国文联、中国民协正式命名四川省遂宁市为“中国观音文化之乡”.
下表为2014年至2018年观音文化故里某土特产企业的线下销售额(单位:万元)
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
线下销售额 | 90 | 170 | 210 | 280 | 340 |
为了解“祝福观音、永保平安”活动的支持度.某新闻调查组对40位老年市民和40位年轻市民进行了问卷调查(每位市民从“很支持”和“支持”中任选一种),其中很支持的老年市民有30人,支持的年轻市民有15人.
(1)从以上5年中任选2年,求其销售额均超过200万元的概率;
(2)请根据以上信息列出列联表,并判断能否有85%的把握认为支持程度与年龄有关.
附:![]() ,其中
,其中![]()
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |