题目内容
【题目】已知数列![]() ,则“存在常数
,则“存在常数![]() ,对任意的
,对任意的![]() ,且
,且![]() ,都有
,都有![]() ”是“数列
”是“数列![]() 为等差数列”的( )
为等差数列”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】C
【解析】
由等差数列的定义不妨令m=n+1,则有:an+1﹣an=c,可知,数列{an}是以c为公差的等差数列,由等差数列的通项公式an=a1+(n﹣1)d,am=a1+(m﹣1)d,(d为公差)得:![]() ,故得解.
,故得解.
①由已知:“存在常数c,对任意的m,n∈N*,且m≠n,都有![]() ”
”
不妨令m=n+1,则有:an+1﹣an=c,由等差数列的定义,
可知,数列{an}是以c为公差的等差数列,
②由“数列{an}为等差数列”则an=a1+(n﹣1)d,am=a1+(m﹣1)d,(d为公差)
所以:![]() ,
,
即存在“存在常数c,对任意的m,n∈N*,且m≠n,都有![]() ”此时,c=d,
”此时,c=d,
综合①②得:“存在常数c,对任意的m,n∈N*,且m≠n,都有![]() ”
”
是“数列{an}为等差数列”的充分必要条件,
故选:C.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15-65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
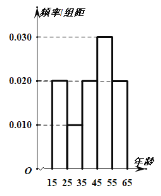
(1)由以上统计数据填2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]() .
.
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动、现从这8人中随机抽2人.记抽到45岁以上的人数为X,求随机变量X的分布列及数学期望.

