题目内容
若函数f(x)＝x3－3x＋a有3个不同的零点，则实数a的取值范围是（ ）
| A．(－2,2) | B．[－2,2] | C．(-1,1) | D．[-1,1] |
A
函数f(x)＝x3－3x＋a有3个不同的零点
方程x3－3x＋a=0有三个不同的根
a=-x3+3x函数g(x)=a与函数F(x)=-x3+3x的图象有三个不同的交点
∵F′(x)＝-3x2+3=-3(x2-1)=-3(x-1)(x+1)
∴即F(x)在x=1处取得极大值2,在x=-1处取得极小值-2
∵直线g(x)=a与函数F(x)=-x3+3x的图象有三个不同的交点
∴a∈(－2,2)
方程x3－3x＋a=0有三个不同的根a=-x3+3x函数g(x)=a与函数F(x)=-x3+3x的图象有三个不同的交点∵F′(x)＝-3x2+3=-3(x2-1)=-3(x-1)(x+1)
∴即F(x)在x=1处取得极大值2,在x=-1处取得极小值-2
∵直线g(x)=a与函数F(x)=-x3+3x的图象有三个不同的交点
∴a∈(－2,2)
练习册系列答案
相关题目
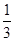x3－x2－3x－1的图象与x轴的交点个数是________．
的方程
在区间
上有两个不同的实数解，则
的取值范围为 .
＝2；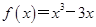
的图象与直线
有相异三个公共点，则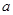
的取值范围是(－2,2)
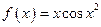在区间[0，4]上的零点个数为（ ）
，
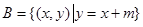，且
，则实数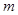
的取值范围是_______________．