题目内容
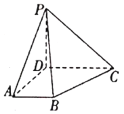
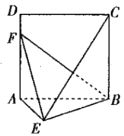
【题目】如图,![]() 是边长为2的正方形,
是边长为2的正方形,![]() 平面
平面![]() ,且
,且![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)线段![]() 上是否存在一点
上是否存在一点![]() ,使二而角
,使二而角![]() 等于45°?若存在,请找出点
等于45°?若存在,请找出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(Ⅰ)详见解析;(Ⅱ)存在点![]() ,当
,当![]() 时,二面角
时,二面角![]() 所成角为
所成角为![]() .
.
【解析】
(Ⅰ)要证得结论只需证得![]() 平面
平面![]() 即可,根据线面垂直判定定理可证得结论;
即可,根据线面垂直判定定理可证得结论;
(Ⅱ)以![]() 为坐标原点建立空间直角坐标系,假设线段
为坐标原点建立空间直角坐标系,假设线段![]() 上存在一点
上存在一点![]() 满足题意,利用二面角的向量求法可构造方程求得
满足题意,利用二面角的向量求法可构造方程求得![]() 点坐标,得到
点坐标,得到![]() 的长.
的长.
(Ⅰ)![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
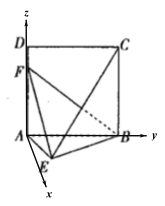
(Ⅱ)如图所示,以![]() 为坐标原点建立空间直角坐标系
为坐标原点建立空间直角坐标系![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,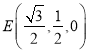 ,
,
假设线段![]() 上存在一点
上存在一点![]() 满足题意,设
满足题意,设![]() ,
,![]() ,
,
![]() 轴
轴![]() 平面
平面![]() ,
,![]() 平面
平面![]() 的一个法向量
的一个法向量![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,而
,而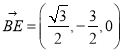 ,
,![]() ,
,
则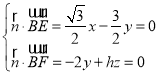 ,令
,令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
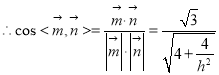 ,
,
若二面角![]() 所成角为
所成角为![]() ,
,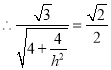 ,解得:
,解得:![]() ,
,
![]() 存在点
存在点![]() ,当
,当![]() 时,二面角
时,二面角![]() 所成角为
所成角为![]() .
.

练习册系列答案
相关题目
【题目】对于某种类型的口服药,口服![]() 小时后,由消化系统进入血液中药物浓度
小时后,由消化系统进入血液中药物浓度![]() (单位)与时间
(单位)与时间![]() 小时的关系为
小时的关系为![]() ,其中
,其中![]() ,
,![]() 为常数,对于某一种药物
为常数,对于某一种药物![]() ,
,![]() ,
,![]() .
.
(1)口服药物后______小时血液中药物浓度最高;
(2)这种药物服药![]() 小时后血液中药物浓度如下表
小时后血液中药物浓度如下表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0.9545 | 0.9304 | 0.6932 | 0.4680 | 0.3010 | 0.1892 | 0.1163 | 0.072 |
一个病人上午8:00第一次服药,要使得病人血液中药物浓度保持在0.5个单位以上,第三次服药时间是______(时间以整点为准)