题目内容
4.一个正方形花圃,被分为n(n≥3,n∈N*)份,种植红、黄、蓝、绿4种颜色不同的花,要求相邻两部分种植不同颜色的花.(1)如图1,正方形被分为3份A、B、C,有多少种不同的种植方法?
(2)如图2,正方形被分为4份A、B、C、D,有多少种不同的种植方法?
(3)如图3,正方形被分为5份A、B、C、D、E,有多少种不同的种植方法?
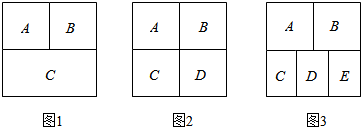
分析 (1)图1,根据题意,分别求出A部分、B部分、C部分种植情况的数目,由分步计数原理计算可得答案;
(2)图2,根据题意,分3步分析,先对A部分种植,再对B部分种植,由图分析易得A、B的种植方法数目,对C种植进行分“与B相同”与“与B不相同”2种情况讨论,最后分析D有2种不同的种植方法,由分步计数原理计算可得答案;
(3)图3,根据题意,分3步分析,先对A部分种植,再对B部分种植,由图分析易得A、B的种植方法数目,对C种植进行分“与B相同”与“与B不相同”2种情况讨论,依次求出D、E的情况数目,利用分类加法原理可得C部分种植方法数目,由分步计数原理计算可得答案.
解答 解:(1)图1,运用分步种植的方法,
先对A部分种植,有4种不同的种植方法;
再对B部分种植,有3种不同的种植方法;
最后对C部分种植,有2种不同的种植方法,
共4×3×2=24种. …(5分)
(2)图2,先对A部分种植,有4种不同的种植方法;
再对B部分种植,有3种不同的种植方法;
对C种植进行分类:若与B相同,D有3种不同的种植方法,共有4×3×1×3=36种种植方法,
若与B不同,C有2种不同的种植方法,D有2种不同的种植方法,
C部分共有4×3×2×2=48.
共有36+48=84种不同的种植方法. …(10分)
(3)图3,先对A部分种植,有4种不同的种植方法;
再对B部分种植,有3种不同的种植方法;
对C部分种植进行分类:若与B相同,D有2种不同的种植方法,E有2种不同的种植方法,共有4×3×1×2×2=48种种植方法,
若与B不同,C有2种不同的种植方法,D有1种不同的种植方法,E有2种不同的种植方法,
C部分共有4×3×2×1×2=48.
共有48+48=96种不同的种植方法.…(16分)
点评 本题考查排列、组合的综合运用,关键是认真分析题目中各部分之间的位置关系,从而利用分类、分步计数原理解答.

| A. | 5 | B. | $2\sqrt{5}$ | C. | 20 | D. | 4$\sqrt{5}$ |
| A. | 4 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 8 |
| A. | $\frac{4}{3}$ | B. | -3 | C. | $\frac{1}{3}$ | D. | 3 |
| A. | (0,$\frac{5}{7}$) | B. | ($\frac{3}{7}$,$\frac{5}{7}$) | C. | (0,$\frac{3}{7}$) | D. | ($\frac{2}{7}$,1) |
