题目内容
【题目】甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取5次,记录如下:
甲 | 88 | 89 | 92 | 90 | 91 |
乙 | 84 | 88 | 96 | 89 | 93 |
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适?请说明理由.(用样本数据特征来说明.)
【答案】解:(Ⅰ)作出茎叶图如下: 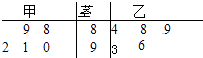 ,
,
(Ⅱ)派甲参赛比较合适,
理由如下 ![]() ,
,![]() ,
,![]() =
= ![]() [(88﹣90)2+(89﹣90)2+(90﹣90)2+(91﹣90)2+(92﹣90)2]=2,
[(88﹣90)2+(89﹣90)2+(90﹣90)2+(91﹣90)2+(92﹣90)2]=2,![]() =
= ![]() [(84﹣90)2+(88﹣90)2+(89﹣90)2+(93﹣90)2+(96﹣90)2]=17.2,
[(84﹣90)2+(88﹣90)2+(89﹣90)2+(93﹣90)2+(96﹣90)2]=17.2,
∵ ![]() ,
, ![]() <
< ![]() ,
,
∴从质量的稳定性角度考虑,采购甲药厂的产品比较合适
【解析】(Ⅰ)作出茎叶图即可;(Ⅱ)分别计算平均数和方差,通过比较平均数和方差的大小,即可得到结论.
【考点精析】认真审题,首先需要了解平均数、中位数、众数(⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据),还要掌握极差、方差与标准差(标准差和方差越大,数据的离散程度越大;标准差和方程为0时,样本各数据全相等,数据没有离散性;方差与原始数据单位不同,解决实际问题时,多采用标准差)的相关知识才是答题的关键.

【题目】有三个游戏规则如表,袋子中分别装有形状、大小相同的球,从袋中无放回地取球,
游戏1 | 游戏2 | 游戏3 |
袋中装有3个黑球和2个白球 | 袋中装有2个黑球和2个白球 | 袋中装有3个黑球和1个白球 |
从袋中取出2个球 | 从袋中取出2个球 | 从袋中取出2个球 |
若取出的两个球同色,则甲胜 | 若取出的两个球同色,则甲胜 | 若取出的两个球同色,则甲胜 |
若取出的两个球不同色,则乙胜 | 若取出的两个球不同色,则乙胜 | 若取出的两个球不同色,则乙胜 |
问其中不公平的游戏是( )
A.游戏2
B.游戏3
C.游戏1和游戏2
D.游戏1和游戏3