题目内容
【题目】已知函数f(x)=ex-ax-1(e为自然对数的底数),a>0.
(1)若函数f(x)恰有一个零点,证明:aa=ea-1;
(2)若f(x)≥0对任意x∈R恒成立,求实数a的取值集合.
【答案】(1)见解析;(2){1}.
【解析】
试题(1)先判断f(x)的单调性,根据“f(x)前有一个零点”,找到关于a的等式,化简整理可得需证结论;(2)根据(1),只需f(x)的最小值不小于0即可.
试题解析:(1)证明: 由![]() ,得
,得![]() .
.
由![]() >0,即
>0,即![]() >0,解得x>lna,同理由
>0,解得x>lna,同理由![]() <0解得x<lna,
<0解得x<lna,
∴ f(x)在(-∞,lna)上是减函数,在(lna,+∞)上是增函数,
于是f(x)在x=lna取得最小值.
又∵ 函数f(x)恰有一个零点,则![]() ,
,
即![]() .
.
化简得:![]() ,
,
∴![]() .
.
(2)解:由(1)知,![]() 在
在![]() 取得最小值
取得最小值![]() ,
,
由题意得![]() ≥0,即
≥0,即![]() ≥0,
≥0,
令![]() ,则
,则![]() ,
,
由![]() 可得0<a<1,由
可得0<a<1,由![]() 可得a>1.
可得a>1.
∴ h(a)在(0,1)上单调递增,在(1,+∞)上单调递减,即![]() ,
,
∴ 当0<a<1或a>1时,h(a)<0,
∴ 要使得f(x)≥0对任意x∈R恒成立,a=1
∴ a的取值集合为{1}

练习册系列答案
相关题目
【题目】某市食品药品监督管理局开展2020年春季快递餐饮安全检查,对本市的8个快递配餐点进行了原料采购加工标准和卫生标准的检查和评分,其评分情况如表所示:
快递配餐点编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采购加工标准评分 | 82 | 75 | 70 | 66 | 83 | 93 | 95 | 100 |
卫生标准评分 | 81 | 79 | 77 | 75 | 82 | 83 | 84 | 87 |
(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(精确到0.1)
的线性回归方程;(精确到0.1)
(2)现从8个被检查点中任意抽取两个组成一组,若两个点的原料采购加工标准和卫生标准的评分均超过80分,则组成“快递标兵配餐点”,求该组被评为“快递标兵配餐点”的概率.
参考公式: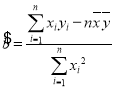 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() .
.
