题目内容
(本小题满分12分)
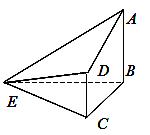
如图,在四棱锥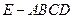 中,
中,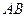 ⊥平面
⊥平面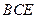 ,
,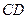 ⊥平面
⊥平面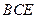 ,
,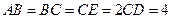 ,
,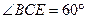 .
.
(1) 证明: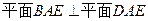 ;
;
(2) 点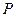 为线段
为线段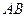 上一点,求直线
上一点,求直线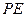 与平面
与平面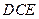 所成角的取值范围.
所成角的取值范围.

如图,在四棱锥
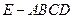 中,
中,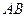 ⊥平面
⊥平面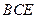 ,
,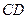 ⊥平面
⊥平面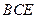 ,
,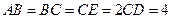 ,
,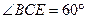 .
. (1) 证明:
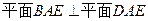 ;
;(2) 点
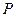 为线段
为线段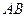 上一点,求直线
上一点,求直线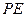 与平面
与平面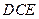 所成角的取值范围.
所成角的取值范围.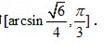
18.解法1:取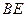 的中点
的中点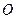 ,连
,连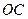 .
.
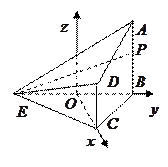
∵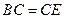 ,∴
,∴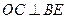 . 又
. 又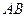 ⊥平面
⊥平面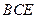 .
.
以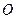 为原点建立空间直角坐标系
为原点建立空间直角坐标系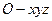 ,如图,
,如图,
则已知条件有: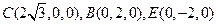 ,
,
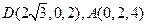 ……………………………………2分
……………………………………2分
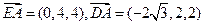 .
.
设平面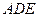 的法向量为
的法向量为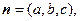
则由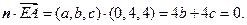
及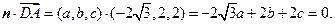
解得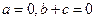 .可取
.可取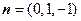 …………………4分
…………………4分
又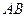 ⊥平面
⊥平面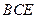 . ∴
. ∴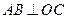 .又
.又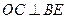 ,∴
,∴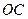 ⊥平面
⊥平面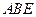 .
.
∴平面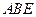 的法向量可取为
的法向量可取为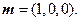
∵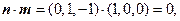 ∴
∴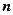 ⊥
⊥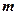 ,∴
,∴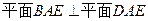 . ………6分
. ………6分
(2)平面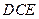 的一个法向量记为
的一个法向量记为 ,
,
则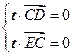 ,即
,即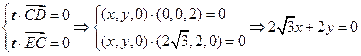

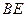 的中点
的中点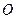 ,连
,连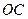 .
.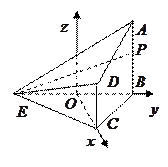
∵
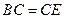 ,∴
,∴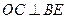 . 又
. 又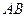 ⊥平面
⊥平面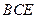 .
.以
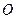 为原点建立空间直角坐标系
为原点建立空间直角坐标系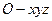 ,如图,
,如图,则已知条件有:
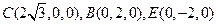 ,
,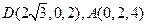 ……………………………………2分
……………………………………2分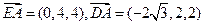 .
.设平面
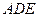 的法向量为
的法向量为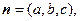
则由
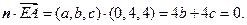
及
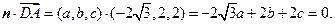
解得
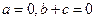 .可取
.可取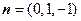 …………………4分
…………………4分又
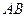 ⊥平面
⊥平面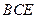 . ∴
. ∴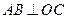 .又
.又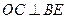 ,∴
,∴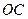 ⊥平面
⊥平面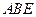 .
.∴平面
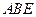 的法向量可取为
的法向量可取为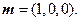
∵
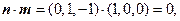 ∴
∴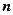 ⊥
⊥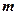 ,∴
,∴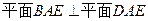 . ………6分
. ………6分(2)平面
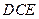 的一个法向量记为
的一个法向量记为 ,
,则
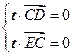 ,即
,即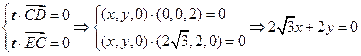


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如右图所示,已知正方形
如右图所示,已知正方形 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直,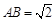 ,AF = 1,M是线段
,AF = 1,M是线段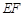 的中点.
的中点.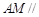 平面
平面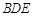 ;
;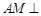 平面
平面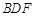 ;
;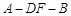 的大小.
的大小.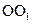 内有一个三棱柱
内有一个三棱柱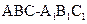 ,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。
,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。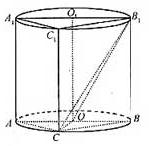
 平面
平面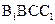 ;
;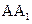 ,在圆柱
,在圆柱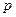 。
。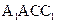 与平面
与平面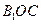 所成的角为
所成的角为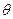
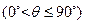 ,当
,当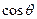 的值。
的值。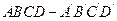 为正方体, 点
为正方体, 点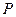 在
在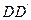 的延长线上,
的延长线上,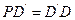 ,
,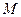 、
、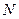 分别为
分别为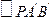 和
和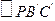 的重心.
的重心. )已知
)已知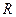 为棱
为棱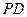 上任意一点,求证:
上任意一点,求证: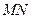 ∥面
∥面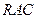 ;
; 的大
的大 小.
小. 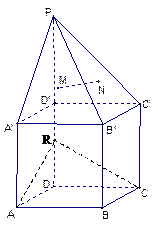
 中,
中,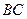 ∥
∥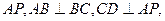
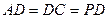 =2,
=2,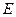 、
、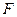 、
、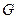 分别是
分别是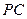 、
、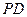 、
、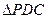 沿
沿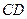 折起,使平面
折起,使平面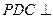 平面
平面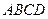 (如图2).
(如图2).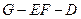 的大小;
的大小;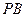 上确定一点
上确定一点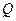 ,使
,使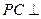 平面
平面 ,并给出证明过程.
,并给出证明过程.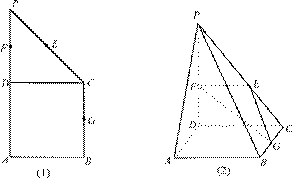
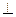 BC,PC
BC,PC 和两条直线a、b,则下列命题中正确的是
和两条直线a、b,则下列命题中正确的是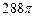 的球内有一个内接正三棱锥
的球内有一个内接正三棱锥 ,球心恰好在底面正△
,球心恰好在底面正△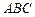 内,一个动点从
内,一个动点从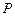 点出发沿球面运动,经过其余三点后返回,则经过的最短路程为__________
点出发沿球面运动,经过其余三点后返回,则经过的最短路程为__________