题目内容
已知抛物线C: 的焦点为F,过点
的焦点为F,过点 的直线
的直线 与C相交于A、B两点,点A关于
与C相交于A、B两点,点A关于 轴的对称点为D。设
轴的对称点为D。设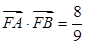 ,则
,则 的内切圆的半径r=___________
的内切圆的半径r=___________
 的焦点为F,过点
的焦点为F,过点 的直线
的直线 与C相交于A、B两点,点A关于
与C相交于A、B两点,点A关于 轴的对称点为D。设
轴的对称点为D。设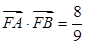 ,则
,则 的内切圆的半径r=___________
的内切圆的半径r=___________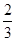
此题考查抛物线及其性质的应用、直线与圆锥曲线相交处理的方法、三角形内切圆的知识、考查学生的逻辑推理和运算求解能力;根据抛物线方程求得焦点坐标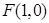 ,设
,设 与C 的交点
与C 的交点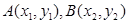 ,所以
,所以 ,则
,则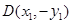 ,设过点
,设过点 的直线
的直线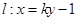 ,代入抛物线方程,整理得
,代入抛物线方程,整理得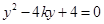 ,所以
,所以 ,所以
,所以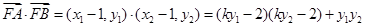
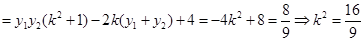 ,所以
,所以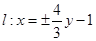 ;又因为
;又因为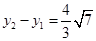 ,直线BD的斜率
,直线BD的斜率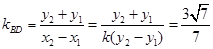 ,所以直线
,所以直线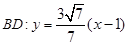 ;又因为点A和点D关于
;又因为点A和点D关于 轴的对称,所以
轴的对称,所以 的平分线是
的平分线是 ,所以
,所以 的内切圆的圆心在
的内切圆的圆心在 轴上,所以设圆心为
轴上,所以设圆心为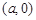 ,且到直线
,且到直线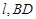 的距离相等,即
的距离相等,即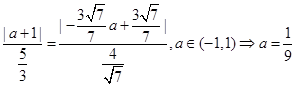 ,所以半径
,所以半径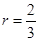
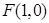 ,设
,设 与C 的交点
与C 的交点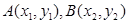 ,所以
,所以 ,则
,则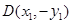 ,设过点
,设过点 的直线
的直线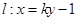 ,代入抛物线方程,整理得
,代入抛物线方程,整理得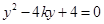 ,所以
,所以 ,所以
,所以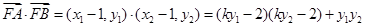
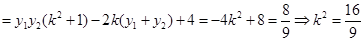 ,所以
,所以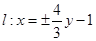 ;又因为
;又因为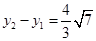 ,直线BD的斜率
,直线BD的斜率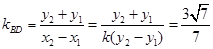 ,所以直线
,所以直线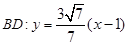 ;又因为点A和点D关于
;又因为点A和点D关于 轴的对称,所以
轴的对称,所以 的平分线是
的平分线是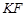 ,所以
,所以 的内切圆的圆心在
的内切圆的圆心在 轴上,所以设圆心为
轴上,所以设圆心为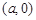 ,且到直线
,且到直线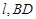 的距离相等,即
的距离相等,即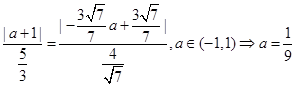 ,所以半径
,所以半径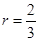

练习册系列答案
相关题目
 的焦点
的焦点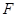 的直线
的直线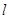 交
交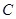 于
于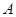 、
、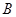 两点(点
两点(点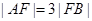 ,则
,则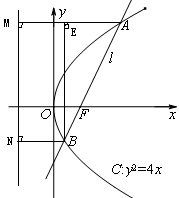
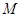 到点
到点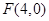 的距离比它到定直线
的距离比它到定直线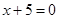 的距离小1,则点
的距离小1,则点 与抛物线
与抛物线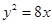 只有一个公共点的直线有 ( )
只有一个公共点的直线有 ( )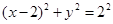 的圆心恰是抛物线的焦点,
的圆心恰是抛物线的焦点,
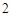 ,且过抛物线焦点,它依次截抛物线和圆于
,且过抛物线焦点,它依次截抛物线和圆于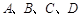 四点,求
四点,求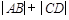 的值.
的值. 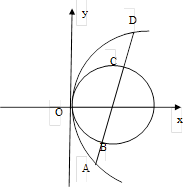
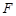 是抛物线
是抛物线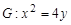 的焦点.
的焦点.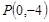 作抛物线
作抛物线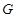 的切线,求切线方程;
的切线,求切线方程;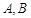 为抛物线
为抛物线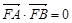 ,延长
,延长 分别交抛物线
分别交抛物线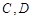 ,求四边形
,求四边形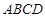 面积的最小值.
面积的最小值.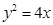 的焦点作直线交抛物线于
的焦点作直线交抛物线于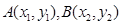 两点,如果
两点,如果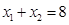 ,那么
,那么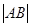 等于( )
等于( ) 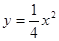 的焦点坐标是
的焦点坐标是