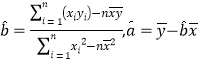题目内容
【题目】设函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的单调性;
的单调性;
(3)当![]() ,且
,且![]() 时证明不等式:
时证明不等式: ![]()
【答案】(Ⅰ)![]() .(Ⅱ)见解析(Ⅲ)见解析
.(Ⅱ)见解析(Ⅲ)见解析
【解析】试题分析:(Ⅰ)代入![]() 时,求得
时,求得![]() ,求得切线的斜率,即可求解切线的方程;
,求得切线的斜率,即可求解切线的方程;
(Ⅱ)求得![]() 的表达式,分
的表达式,分![]() 和
和![]() 和
和![]() 三种情况分类讨论,即可求解函数
三种情况分类讨论,即可求解函数![]() 的单调区间;
的单调区间;
(Ⅲ)先由![]() 时,证得
时,证得![]() ,再取
,再取![]() 得
得![]() ,进而可证明上述不等式.
,进而可证明上述不等式.
试题解析:
(Ⅰ)解:当![]() 时,
时, ![]() ,
,
所以,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅱ)解:函数![]() .
.
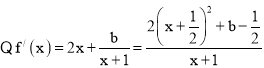 ,
,
分以下几种情形讨论:
(1)当![]() 时,
时, ![]() ,函数
,函数![]() ;
;
(2)当![]() 时,
时, ![]() ,
,
①当![]() 时,
时, ![]() ,
,
![]() ,
,
所以,函数![]()
②当![]() 时,
时, ![]()
![]()
![]() ,
,
所以, ![]() .
.
(Ⅲ)证明:当![]() -1时,
-1时, ![]() ,
,
令![]() ,则
,则![]() 在
在![]() 上恒正,
上恒正,
所以, ![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时,恒有
时,恒有![]() ,
,
即当![]() 时,
时, ![]() ,
,
对任意正整数![]() ,取
,取![]() 得
得![]() ,
,
所以, ![]()
= ![]()
= ![]()
![]()
=![]()

练习册系列答案
相关题目
【题目】某厂需要确定加工某大型零件所花费的时间,连续4天做了4次统计,得到的数据如下:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 5.5 |
(1)在直角坐标系中画出以上数据的散点图,求出![]() 关于
关于![]() 的回归方程
的回归方程![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(2)试预测加工10个零件需要多少时间?
参考公式:两个具有线性关系的变量的一组数据:![]() ,
,
其回归方程为![]() ,其中
,其中