题目内容
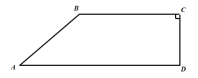
【题目】如图,某山地车训练中心有一直角梯形森林区域![]() ,其四条边均为道路,其中
,其四条边均为道路,其中![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,
千米,![]() 千米.现有甲、乙两名特训队员进行野外对抗训练,要求同时从
千米.现有甲、乙两名特训队员进行野外对抗训练,要求同时从![]() 地出发匀速前往
地出发匀速前往![]() 地,其中甲的行驶路线是
地,其中甲的行驶路线是![]() ,速度为
,速度为![]() 千米/小时,乙的行驶路线是
千米/小时,乙的行驶路线是![]() ,速度为
,速度为![]() 千米/小时.
千米/小时.
(1)若甲、乙两名特训队员到达![]() 地的时间相差不超过
地的时间相差不超过![]() 分钟,求乙的速度
分钟,求乙的速度![]() 的取值范围;
的取值范围;
(2)已知甲、乙两名特训队员携带的无线通讯设备有效联系的最大距离是![]() 千米.若乙先于甲到达
千米.若乙先于甲到达![]() 地,且乙从
地,且乙从![]() 地到
地到![]() 地的整个过程中始终能用通讯设备对甲保持有效联系,求乙的速度
地的整个过程中始终能用通讯设备对甲保持有效联系,求乙的速度![]() 的取值范围.
的取值范围.
【答案】(1)乙的速度ν的取值范围为![]() ,(单位千米/小时)(2)
,(单位千米/小时)(2)![]()
【解析】
(1)过点B作直线AD的垂线,垂足为E.分别求得甲、乙的运动时间,列不等式求解即可
(2)讨论乙运动到AB,BC,CD时,甲、乙之间的距离的平方为![]() 的表达式,求函数最值,列不等式求解即可
的表达式,求函数最值,列不等式求解即可
(1)如图.过点B作直线AD的垂线,垂足为E.
因为四边形ABCD为直角梯形,所以四边形EBCD为矩形,则![]() ,
,![]() ,
,
又在直角三角形ABE中,![]() ,即
,即![]()
则由题意得,甲从A地出发匀速前往D地所需时间为![]() (小时),
(小时),
乙从A地出发匀速前往D地所需时间为![]() (小时),
(小时),
由题意可知![]() ,即
,即![]() ,解得
,解得![]() ,
,
所求乙的速度ν的取值范围为![]() ,(单位千米/小时).
,(单位千米/小时).
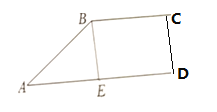
(2)设经过t小时,甲、乙之间的距离的平方为![]() 千米,
千米,
由于乙先于甲到达D地,所以![]() ,解得
,解得![]() ,
,
①当![]() 时,即
时,即![]() 时,
时,
![]()
因为![]() ,所以当
,所以当![]() 时,
时,![]() 取得最大值,
取得最大值,
且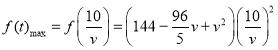 ,
,
由题意可得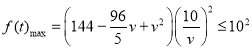 ,解得
,解得![]() ,
,
②当![]() 时,即
时,即![]() 时,
时,
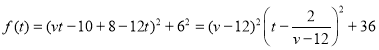 ,
,
因为![]() ,所以
,所以![]() ,则当
,则当![]() 时,
时,![]() 取得最大值,
取得最大值,
且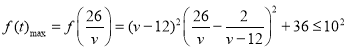 ,解得
,解得![]()
③当![]() 时,即
时,即![]() 时,
时,
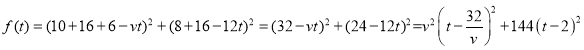 ,
,
因为![]() ,所以
,所以![]() ,
,
则函数![]() 在区间
在区间![]() 上单调递减,即当
上单调递减,即当![]() 时,
时,![]() 取得最大值,
取得最大值,
且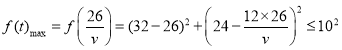 ,解得
,解得![]() ,
,
由①②③同时成立可得![]() ,又因为
,又因为![]() ,所以
,所以![]()
即所求乙的速度v的取值范围为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】微信作为一款社交软件已经在支付、理财、交通、运动等各方面给人们的生活带来各种各样的便利.手机微信中的“微信运动”,不仅可以看自己每天的运动步数,还可以看到朋友圈里好友的步数.![]() 先生朋友圈里有大量好友使用了“微信运动”这项功能,他随机选取了其中40名,记录了他们某一天的走路步数,统计数据如下表所示:
先生朋友圈里有大量好友使用了“微信运动”这项功能,他随机选取了其中40名,记录了他们某一天的走路步数,统计数据如下表所示:
步数 性别 |
|
|
|
|
|
|
男 | 3 | 4 | 5 | 4 | 3 | 1 |
女 | 3 | 5 | 3 | 2 | 5 | 2 |
(1)以样本估计总体,视样本频率为概率,在![]() 先生的微信朋友圈里的男性好友中任意选取3名,其中走路步数不低于6000步的有
先生的微信朋友圈里的男性好友中任意选取3名,其中走路步数不低于6000步的有![]() 名,求
名,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)如果某人一天的走路步数不低于8000步,此人将被“微信运动”评定为“运动达人”,否则为“运动懒人”.根据题意完成下面的2×2列联表,并据此判断能否有90%以上的把握认为“评定类型”与“性别”有关?
运动达人 | 运动懒人 | 总计 | |
男 | |||
女 | |||
总计 |
附: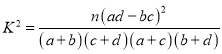 ,其中
,其中![]()
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |