Question

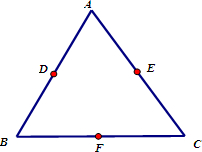（2012•江苏一模）如图，已知面积为1的正三角形ABC三边的中点分别为D、E、F，从A，B，C，D，E，F六个点中任取三个不同的点，所构成的三角形的面积为X（三点共线时，规定X=0）
（1）求P(X≥

1

2

)；
（2）求E（X）

Answer 1

分析：（1）从六点中任取三个不同的点共有

C

3 6

=20个基本事件，事件“X≥

1

2

”所含基本事件有2×3+1=7，故可求P(X≥

1

2

)；
（2）X的取值为0，

1

4

，

1

2

，1，求出相应的概率，即可得到X的分布列，从而可求数学期望．

解答：解：（1）从六点中任取三个不同的点共有

C

3 6

=20个基本事件，
事件“X≥

1

2

”所含基本事件有2×3+1=7，
从而P(X≥

1

2

)=

7

20

．（5分）
（2）X的取值为0，

1

4

，

1

2

，1，
P（X=0）=

3

C 3 6

=

3

20

；P（X=

1

4

）=

10

20

；P（X=

1

2

）=

6

20

；P（X=1）=

1

20

分布列为：

X	0	1 4	1 2	1
P	3 20	10 20	6 20	1 20

则E(X)=0×

3

20

+

1

4

×

10

20

+

1

2

×

6

20

+1×

1

20

=

13

40

．
答：P(X≥

1

2

)=

7

20

，E(X)=

13

40

．（10分）

点评：本题考查离散型随机变量的期望，考查概率的计算，解题的关键是确定变量的取值，计算其概率．