题目内容
（2012•江苏一模）观察下列等式：
13=1，
13+23=9，
13+23+33=36，
13+23+33+43=100
…
猜想：13+23+33+43+…+n3=
13=1，
13+23=9，
13+23+33=36，
13+23+33+43=100
…
猜想：13+23+33+43+…+n3=
[
]2
| n(n+1) |
| 2 |
[
]2
（n∈N*）．| n(n+1) |
| 2 |
分析：观察等式右边的数的规律，从中发现右边数是（1+2+3++n）2，从而可求出所求．
解答：解：将这些算式进行整理．13=1，13+23=9=32=（1+2）3，
13+23+33=36=62=（1+2+3）2，13+23+33+43=100=102=（1+2+3+4）2，
由以上规律可得
13+23+33+…+n3=（1+2+3++n）2=[
]2．
故答案为：[
]2
13+23+33=36=62=（1+2+3）2，13+23+33+43=100=102=（1+2+3+4）2，
由以上规律可得
13+23+33+…+n3=（1+2+3++n）2=[
| n(n+1) |
| 2 |
故答案为：[
| n(n+1) |
| 2 |
点评：本题主要考查合情推理能力和等差数列知识，提醒学生从等号右侧数都为平方数入手寻找发现规律，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
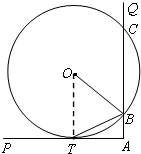（2012•江苏一模）选修4-1：几何证明选讲