题目内容
（2012•江苏一模）选修4-1：几何证明选讲如图，∠PAQ是直角，圆O与AP相切于点T，与AQ相交于两点B，C．
求证：BT平分∠OBA．
分析：连结OT，说明OT⊥AP．证明∠TBA=∠BTO．再证明∠OBT=∠TBA，即可证明BT平分∠OBA．
解答：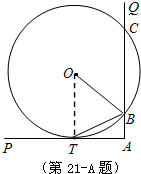
证明：连结OT，因为AT是切线，所以OT⊥AP．
又因为∠PAQ是直角，即AQ⊥AP，所以AB∥OT，所以∠TBA=∠BTO．
又OT=OB，所以∠OTB=∠OBT，
所以∠OBT=∠TBA，
即BT平分∠OBA．
证明：连结OT，因为AT是切线，所以OT⊥AP．又因为∠PAQ是直角，即AQ⊥AP，所以AB∥OT，所以∠TBA=∠BTO．
又OT=OB，所以∠OTB=∠OBT，
所以∠OBT=∠TBA，
即BT平分∠OBA．
点评：本题考查直线与圆相切的性质的应用，平行线内错角相等等知识，考查逻辑推理能力．
练习册系列答案
相关题目