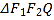题目内容
【题目】由甲、乙、丙三个人组成的团队参加某项闯关游戏,第一关解密码锁,3个人依次进行,每人必须在1分钟内完成,否则派下一个人.3个人中只要有一人能解开密码锁,则该团队进入下一关,否则淘汰出局.根据以往100次的测试,分别获得甲、乙解开密码锁所需时间的频率分布直方图.
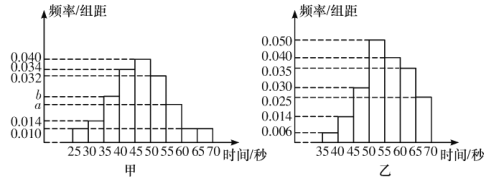
(1)若甲解开密码锁所需时间的中位数为47,求![]() 、
、![]() 的值,并分别求出甲、乙在1分钟内解开密码锁的频率;
的值,并分别求出甲、乙在1分钟内解开密码锁的频率;
(2)若以解开密码锁所需时间位于各区间的频率代替解开密码锁所需时间位于该区间的概率,并且丙在1分钟内解开密码锁的概率为0.5,各人是否解开密码锁相互独立.
①按乙丙甲的先后顺序和按丙乙甲的先后顺序哪一种可使派出人员数目的数学期望更小.
②试猜想:该团队以怎样的先后顺序派出人员,可使所需派出的人员数目![]() 的数学期望达到最小,不需要说明理由.
的数学期望达到最小,不需要说明理由.
【答案】(1)![]() ;
;![]() ;甲在1分钟内解开密码锁的频率是
;甲在1分钟内解开密码锁的频率是![]() ;乙在1分钟内解开密码锁的频率是
;乙在1分钟内解开密码锁的频率是![]() (2)①按乙丙甲派出的顺序期望更小②先派出甲,再派乙,最后派丙
(2)①按乙丙甲派出的顺序期望更小②先派出甲,再派乙,最后派丙
【解析】
(1)根据甲解开密码锁所需时间的中位数求得![]() ,根据频率求得
,根据频率求得![]() ,由此求得甲在1分钟内解开密码锁的频率.通过频率分布直方图求得乙在1分钟内解开密码锁的频率.
,由此求得甲在1分钟内解开密码锁的频率.通过频率分布直方图求得乙在1分钟内解开密码锁的频率.
(2)
①分别求得两个不同顺序的方法对应的数学期望,由此求得期望更小的安排方法.
②按照解锁概率大的人员排前面,期望值最小.通过计算前两位、后两位人员交换时,期望值的变化情况,来确定最优的排法.
(1)甲解开密码锁所需时间的中位数为47,
∴![]()
![]() ,解得
,解得![]() ;
;
∴![]() ,解得
,解得![]() ;
;
∴甲在1分钟内解开密码锁的频率是![]() ;
;
乙在1分钟内解开密码锁的频率是![]() ;
;
(2)由(1)知,甲、乙、丙在1分钟内解开密码锁的概率分别是![]() ,
,![]() ,
,![]() 且各人是否解开密码锁相互独立;
且各人是否解开密码锁相互独立;
设按乙丙甲的顺序对应的数学期望为![]() ,按丙乙甲的顺序对应的数学期望为
,按丙乙甲的顺序对应的数学期望为![]()
则![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,∴
,∴![]() ,
,
①∴![]()
同理可求得![]()
所以按乙丙甲派出的顺序期望更小.
②答案:先派出甲,再派乙,最后派丙,
(下面是理由,给老师和学生参考)
设按先后顺序自能完成任务的概率分别为![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 互不相等,
互不相等,
根据题意知![]() 的取值为1,2,3;
的取值为1,2,3;
则![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,∴
,∴![]() ,
,
若交换前两个人的派出顺序,则变为![]() ,
,
由此可见,当![]() 时,交换前两人的派出顺序会增大均值,故应选概率最大的甲先开锁;
时,交换前两人的派出顺序会增大均值,故应选概率最大的甲先开锁;
若保持第一人派出的人选不变,交换后两人的派出顺序,
∵交换前![]() ,
,
∴交换后的派出顺序则期望值变为![]() ,
,
当![]() 时,交换后的派出顺序可增大均值;所以先派出甲,再派乙,最后派丙,
时,交换后的派出顺序可增大均值;所以先派出甲,再派乙,最后派丙,
这样能使所需派出的人员数目的均值(教学期望)达到最小.