Question

（2012•河北区一模）已知向量

a

=（x+z，3），

b

=（2，y-z），且

a

⊥

b

．若x，y满足不等式|x|+|y|≤1，则z的取值范围为

[-3，3]

．

Answer 1

分析：根据平面向量的垂直的坐标运算法则，我们易根据已知中的条件构造出一个关于x，y，z的方程，即关于Z的目标函数，画了约束条件|x|+|y|≤1对应的平面区域，并求出各个角点的坐标，代入即可求出目标函数的最值，进而给出z的取值范围．

解答：解：∵向量

a

=（x+z，3），

b

=（2，y-z），且

a

⊥

b

，∴

a

•

b

=2x+2z+3y-3z=0，∴z=2x+3y．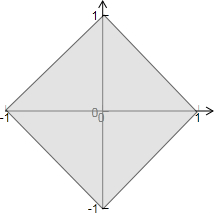
∵满足不等式|x|+|y|≤1的平面区域如下图所示：
由图可知当x=0，y=1时，z取最大值3，
当x=0，y=-1时，z取最小值-3，
故z的取值范围为[-3，3]，
故答案为[-3，3]．

点评：本题考查的知识点是数量积判断两个平面向量的垂直关系，简单线性规划的应用，其中利用平面向量的垂直的坐标运算法则，求出目标函数的解析式是解答本题的关键．